Représenter graphiquement les variations d'une grandeur (cas général)
Exemple :
AJOUTER EXEMPLE
Méthode : Tracer la représentation graphique associée à une relation donnée.
On identifie quelle grandeur joue le rôle de \(y\) et quelle grandeur joue le rôle de \(x\) et on les place sur les axes d'un repère
On identifie la forme de la relation que l'on écrirait en mathématique (par exemple \(y=C\cos(ax)\) )
On identifie alors les paramètres de la fonction "équivalente" et on cherche :
Les valeurs particulières : valeur en \(x=0\) ? valeurs aux limites ?
On place les points remarquables de la représentation graphique associée
On trace la courbe
Attention :
Les grandeurs portées sur les axes sont en général différentes de celles utilisées en mathématiques.
L'altitude \(z\) peut par exemple être portée sur l'axe des abscisses (horizontal)
La position \(x\) est souvent portée sur l'axe des ordonnées (vertical)
Rappel : Fonctions trigonométriques
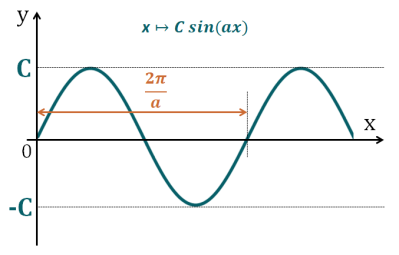
Les fonctions \(x \longmapsto C \cos(ax)\) et \(x \longmapsto C\sin(ax)\) sont des fonctions
Périodiques (=qui se répète)
Avec une période (=longueur de motif) \(\dfrac{2\pi}{a}\)
Dont les valeurs varient entre \(C\) et \(-C\), \(C\) est appelée l'amplitude en physique.
La différence entre les représentations graphiques de ces deux fonctions est leur valeur en zéro. Elles sont décalées d'une demi-période.
La fonction cosinus vaut 1 en 0, et donc la fonction \(x \longmapsto C \cos(ax)\) vaut \(C\) en \(x=0\)
La fonction sinus vaut 0 en 0, et donc la fonction \(x \longmapsto C \sin(ax)\) vaut \(0\) en \(x=0\)