Calculer une intégrale comme l'aire sous la courbe
Exemple : Cinématique
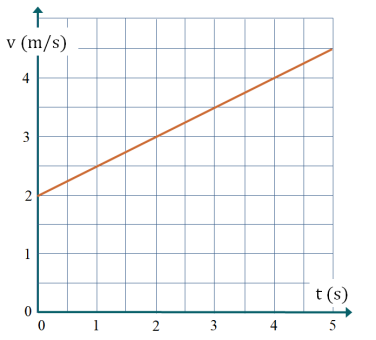
Un mobile considéré comme ponctuel se déplace suivant un axe \((Ox)\). La courbe représentative de la vitesse \(v\) en fonction du temps est représentée par le graphe donné ci-après.
Calculer la distance parcourue (en m) par le mobile entre les dates \(t = 1~\mbox{s}\) et \(t = 4~\mbox{s}\).
On rappelle que : \(v(t) = x'(t)=\dot x (t)\)
Explication :
Il faut calculer \(x(4) - x(1)\) soit \(\displaystyle\int_{1}^{4} x'(t) \text{d}t =\displaystyle\int_{1}^{4} v(t) \text{d}t \)
Il faut évaluer l'aire sous la courbe représentative de \(v\) (en vert sur le schéma ci-dessous) entre les bornes \(t=1~\mbox{s}\) et \(t=4~\mbox{s}\)
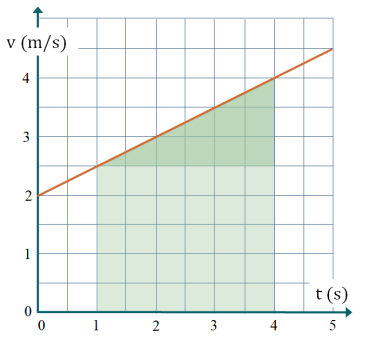
Calcul de l'aire sous la courbe:
On calcule l'aire du rectangle (vert clair) : \(A_{rectangle} = \mbox{Largeur} \times \text{Longueur}\)
On calcule l'aire du triangle (vert foncé) : \(A_{triangle rectangle}= \dfrac{\text{Largeur} \times \text{Longueur}}{2}\)
L'aire sous la courbe correspond à la combinaison des deux aires précédentes : \(A= \text{Largeur} \times \text{Longueur} + \dfrac{\text{Largeur} \times \text{Longueur}}{2} \)
Application numérique : \(A = 3\times2,5 + \dfrac{3\times 1,5}{2} = 7,5 + 2,25 = 9,75 ~\mbox{m}\)
Attention l'aire recherchée s'exprime ici en \(\mbox{m}\) et non en \(\mbox{m}^2\). Il faut en effet prendre en compte les unités de \(v\) (en m/s) et de \(t\) (en s), le produit s'exprime en \(\mbox{m/s} \cdot \mbox{s} = \mbox{m}\) (mètre)
Méthode : Calculer une intégrale en utilisant l'aire sous la courbe
Repérer
La grandeur qui joue le rôle de variable \(x\) (en maths),
La grandeur qui joue le rôle de la fonction (\(f\) en maths reporté sur l'axe des ordonnées)
Dessiner l'aire délimitée par la courbe de la fonction qui est intégrée et par les 2 droites verticales données par les bornes.
Calculer l'aire en identifiant une surface géométrique connue (ou compter les carreaux)
Donner l'unité appropriée en multipliant les unités de l'ordonnée et de l’abscisse.
Conseil :
L'unité d'une aire ou de surface s'exprime usuellement en \(\mbox{m}^2\). Ici l'unité d'aire, non précisée en mathématiques, se détermine par le produit des unités de \(x\) et \(y\).
Attention :
Si la fonction à intégrer est négative, l'intégrale est négative, il convient donc de prendre la valeur absolue pour le résultat de l'aire.
Remarque :
On pourrait modéliser la fonction représentée et calculer sa primitive. Cette résolution analytique peut s'avérer possible mais plus longue.