Utiliser l'échelle linéaire
Exemple : Représentation des interfranges en fonction de la distance dans une situation d'interférences
Un laser monochromatique de longueur d'onde \(\lambda\), éclaire deux fentes de Young séparées par la distance \(a\).
L'écran et les fentes sont éloignés de la distance \(D\).
La figure d'interférence sur l'écran permet de mesurer la distance entre deux franges brillantes sur l'écran que l'on notera « \(i\) » pour interfrange.
On obtient pour une valeur de \(\lambda = 600~\mbox{nm}\), les résultats expérimentaux sont présentés dans le tableau ci-dessous.
\(D\) (cm) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
\(i\) (mm) | 0,0 | 0,5 | 1,2 | 1,9 | 2,5 | 3,0 | 3,5 | 4,2 | 4,9 | 5,3 | 5,9 |
Représenter la taille de l'interfrange \(i\) en fonction de la distance \(D\) entre les fentes et l'écran.
Explication :
On prépare un graphique en dessinant deux axes avec des flèches
On choisit les axes
On détermine la grandeur qui joue le rôle de \(y\) : ici c'est \(i\), et son unité : ici des mm. On écrit donc "\(i\) (mm)" sur l'axe vertical.
On détermine la grandeur qui joue le rôle de \(x\) : ici c'est \(D\), et son unité : ici des cm. On écrit donc "\(D\) (cm)" sur l'axe horizontal.
On choisit l'échelle
On cherche la plus petite et la plus grande valeur de \(D\) : 0 à 100 cm. On place donc le zéro à l'origine du graphe et on place ensuite 100 presque à l'extrémité de l'axe horizontal. Ici prendre 10 cm sur le graphe pour 100 cm semble un bon compromis. On place ensuite les graduations intermédiaires.
On cherche la plus petite et la plus grande valeur de \(i\) : de 0 à 5,9 mm. On place donc aussi le zéro à l'origine du graphe, et on place ensuite le nombre 6 vers l'extrémité de l'axe vertical, si possible un nombre de carreaux pairs après l'origine. Ici prendre 1 cm sur le graphe pour 1 mm d'interfrange semble le bon compromis.
On place les points : on utilise une règle graduée pour placer chacun des points.
On place un tiret au niveau de l'abscisse (valeur sur l'axe des \(x\)) et de l'ordonnée (valeur sur l'axe des \(y\)) du point
On place une croix (symbole \(+\)) au niveau du point.
On met un titre
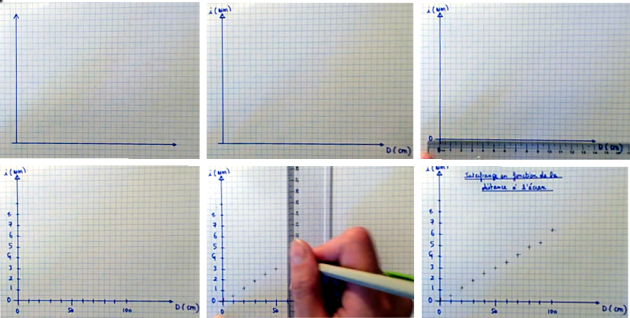
Méthode : Tracer un graphique
Tracer un repère
Définir les axes
Repérer la grandeur qui joue le rôle de \(y\) (axe vertical) et celle qui va jouer le rôle de \(x\) (axe horizontal)
Écrire le nom des grandeurs et indiquer entre parenthèses leur unité
Choisir l'échelle
Regarder la valeur minimale et maximale de chaque grandeur
Choisir une échelle "adaptée" pour utiliser le maximum de l'axe tout en facilitant les calculs
Placer la première et la dernière graduation. Calculer l'échelle. Placer les graduations intermédiaires.
Placer les points
Repérer (on peut placer un tiret) pour chaque point son abscisse et son ordonnée
Avec une règle, placer le point en mettant une croix en forme de +
Mettre un titre
Attention : Valeurs négatives
Si certaines valeurs sont négatives, il faut prévoir d'agrandir le repère vers la gauche ( \(x\) négatifs) ou vers le bas ( \(y\) négatifs)