Déterminer l'équation d'une droite qui coupe l'axe des ordonnées
Exemple : Caractéristique d'un électrolyseur
Les points expérimentaux obtenus en mesurant tension et intensité du courant aux bornes d'un électrolyseur permettent de tracer une droite de régression linéaire raisonnable.
On modélise donc cette tension en fonction de l'intensité par une droite d'équation \(U = E' + r' I\) .
\(U\) est la tension (unité : volt V) aux bornes de l'électrolyseur, \(I\) est l'intensité (unité : ampère A) qui le traverse, \(E'\) est la force contre-électromotrice de l'électrolyseur (unité : volt V) et \(r'\) sa résistance interne (unité : Ohm).
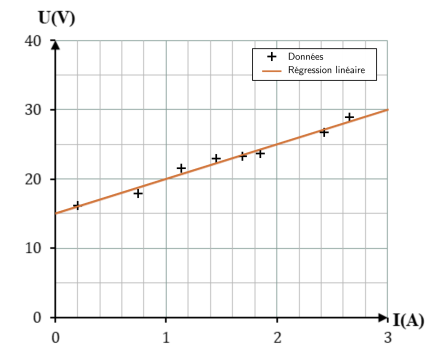
Déterminer les valeurs de \(E'\) et \(r'\).
On rappelle que : \(1~\mbox{V}\cdot\mbox{A}^{-1}=1~\Omega\)
Explication :
Analogie avec la situation mathématique de référence :
Situation de chimie présentée ici \(U = E' + r' I\) | Situation typique de mathématiques \(y=b+a\cdot x\) |
\(U\) | \(y\) : fonction |
\(I\) | \(x\) : variable |
\(r'\) | \(a\) : pente |
\(E'\) | \(b\) : ordonnée à l'origine |
Lecture graphique :
Ordonnée à l'origine : la droite coupe l'axe des ordonnées en \(U=15\) V.
On a donc : \(E'=15\) V.
Pente : On calcule la pente à partir des deux points de la droite :
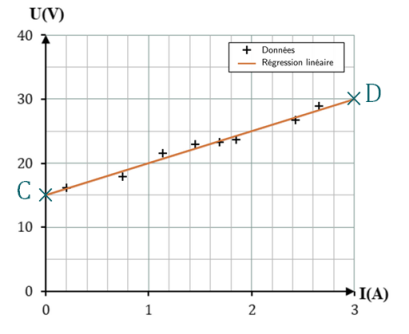
On choisit deux points \(C\) et \(D\) sur la droite (voir graphe ci-après), par exemple : \(C \left(0 \mbox{ A} ;15 \mbox{ V}\right)\) et \(D(3 \mbox{ A} ;30 \mbox{ V})\)
On applique la formule qui permet de déterminer la pente :
pente = \(r'=\dfrac{y_D-y_C}{x_D-x_C}=\dfrac{30\mbox{ V}-15\mbox{ V}}{3\mbox{ A}-0\mbox{ A}}\).
On réalise l'application numérique : \(r'=\dfrac{15}{3}\dfrac{\mbox{V}}{\mbox{A}}=5\dfrac{\mbox{V}}{\mbox{A}}\)
On réalise le changement d'unité : \(r' = 5~\Omega\)
Méthode : Situation de chimie présentée ici
Identifier qui joue le rôle :
de \(y\) : la grandeur dont on étudie la variation
de \(x\) : la grandeur que l'on a fait varier pendant l'expérience
de \(a\) : la pente (aussi appelée coefficient directeur)
de \(b\) : l'ordonnée à l'origine
Déterminer l'ordonnée à l'origine en relevant la valeur à laquelle la droite coupe l'axe vertical.
Déterminer la pente en choisissant deux points sur la droite et en utilisant la formule : \(a = \dfrac{y_D - y_C}{x_D - x_C}\) .
Attention : Les unités
Les grandeurs physiques ont des unités, et donc les paramètres \(a\) et \(b\) aussi.
\(b\) a la même unité que \(y\)
\(a\) a la même unité que \(\dfrac{y}{x}\).
Complément : La droite qui passe par l'origine : situation de proportionnalité
Le cas particulier où \(b=0\) est très courant. La représentation graphique de \(y(x)\) est alors une droite passant par l'origine et les deux grandeurs \(x\) et \(y\) sont proportionnelles.
\(a\) s'appelle alors constante (ou coefficient) de proportionnalité entre \(x\) et \(y\) .
Rappel : Modéliser avec une régression linéaire
En physique, on mesure différentes valeurs d'une grandeur qui varie en fonction d'une autre grandeur (comme par exemple la pression dans un fluide qui varie en fonction de la profondeur). Ces valeurs ne sont pas des nombres exacts au sens des mathématiques puisqu'il y a toujours une incertitude sur la valeur de la mesure.
En physique, on a souvent de bonnes raisons de penser que ces deux valeurs varient en suivant une fonction affine (d'autres types de relations sont possibles).
Dans ce cas, on cherche la droite qui passe le plus proche de tous les points que l'on a mesurés (on peut la dessiner à la main ou utiliser un logiciel)
On obtient alors la meilleure estimation des paramètres de la loi en déterminant l'équation de la droite de régression linéaire.
Rappel : Le sens des paramètres d'une régression linéaire
Dans un modèle affine de la forme \(y=ax+b\),
\(a\) est le coefficient directeur : il indique de combien \(y\) augmente quand \(x\) augmente de 1
Si la droite "monte", \(a\) est positif
Si la droite "descend", \(a\) est négatif
\(b\) est l'ordonnée à l'origine : elle indique quelle est la valeur de \(y\) quand \(x = 0\)
Si la droite passe par l'origine (point de coordonnées ( 0 ; 0 )), alors \(b=0\)