Déterminer l'équation d'une sinusoïde
Exemple : Tension aux bornes d'un dipôle
La tension instantanée aux bornes d'un dipôle électrique est la suivante :
\(U(t) = U_{max} \times \cos \left(\dfrac{2\pi }{T}t\right) + U_{moy}\)
\(U_{max}\) est l'amplitude de la tension alternative (en volts)
\(U_{moy}\) est appelée composante continue (en volts)
\(T\) est la période (en seconde).
On a relevé l'enregistrement suivant :
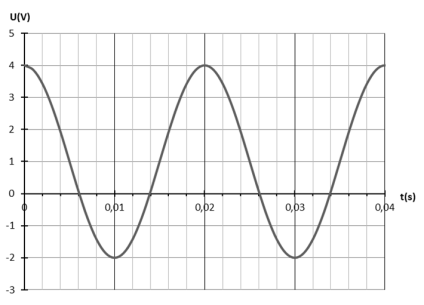
Déterminer les valeurs de \(U_{max}~,~ U_{moy}\) et \(T\) permettant d'écrire \(U(t)\).
Explication :
Analogie avec la situation mathématique de référence :
Situation physique (électricité) présentée ici \(U(t) = U_{max} \times \cos \left(\dfrac{2\pi }{T}t\right) + U_{moy}\) | Situation typique de mathématiques \(y = A \cos \left(\dfrac {2 \pi}{T} x\right) + M\) |
\(U\) | \(y\) : fonction |
\(t\) : temps | \(x\) : variable |
\(U_{max} \) | \(A\) : amplitude |
\(U_{moy}\) : composante continue | \(M\) : valeur moyenne |
La période \(T\) est commune aux deux écritures.
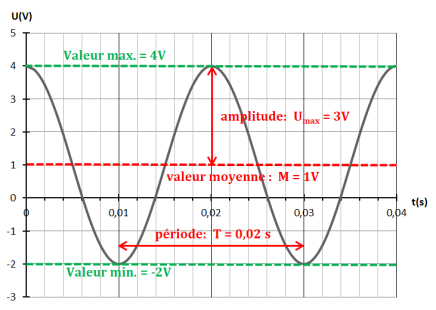
Période : on repère la "longueur" du motif horizontal qui se répète du fait de la périodicité de la fonction cosinus
on peut choisir la "longueur" entre 2 minimums consécutifs ( cf schéma ci-dessous)
La période a donc pour valeur 0,03 - 0,01 = 0,02 s
Amplitude et Moyenne:
on relève les valeurs maximale et minimale sur la courbe :
\(y_{max}= 4 V\) et \( y_{min}= -1 V\)
la demi-différence donne l'amplitude : \(\dfrac {4-(-2)}{2} =3\)
et la demi-somme \(\dfrac {4+(-2)}{2} =1\) donne la moyenne.
Présentation du résultat :
\(U_{max} = 3 V\), puis \(U_{moy}= 1 V\) et \(T = 0,02 s\)
\(U(t) = 3 \cos \left(\dfrac{2\pi }{0,02}t\right) + 1 =3 \cos (100\pi t) + 1\)
Méthode :
Lire les valeurs maximale et minimale de \(y\) (attention à l'échelle)
Calculer les valeurs de :
L'amplitude : \(A = \dfrac{(max - min)}{2}\)
La moyenne : \(M = \dfrac{(min + max)}{2}\)
Détermine la période en mesurant la longueur sur l'axe horizontal du plus petit motif de la courbe qui se répète (attention à l'échelle)
Attention : La définition de l'ampliture
L'amplitude \(A\) a toujours une valeur positive
mais l'amplitude N'est PAS égale
À la valeur maximale de \(y\)
À la distance entre le maximum et le minimum de \(y\) (c'est la moitié)
Complément : Courbe symétrique par rapport à une droite horizontale
Si la courbe représentative de \(y\) est symétrique par rapport à la droite d'équation \(y = M\), alors la moyenne de cette grandeur vaut M.
Si la courbe est symétrique par rapport à l'axe des abscisses , alors la valeur moyenne \(M\) est nulle