Déterminer le temps caractéristique d'une évolution exponentielle (méthode de la tangente)
Exemple : La décharge d'un condensateur
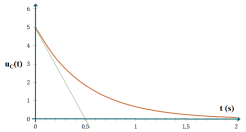
L'évolution temporelle de la tension \(u_{C}\) (unité : volt V) aux bornes d'un condensateur de capacité C lors de sa décharge dans un circuit RC est donnée sur le graphe ci-dessous (en orange).
L'équation horaire de \(u_{C}\) est du type : \(u_{C}(t) = U_{0} \times \text{e}^{-\frac{t}{\tau}}\)
\(\tau\) est la constante de temps (unité: seconde s).
Calculer la valeur de \(\tau\).
Explication :
Lors d'une évolution exponentielle, la valeur du temps caractéristique se lit au croisement de la tangente à l'origine et de l'asymptote de la courbe
Lecture graphique :
Dans ce cas, l'asymptote aux temps longs est l'axe des abscisses
La tangente à l'origine coupe l'axe des abscisses à \(t=0,5~\mbox{s}\)
Le temps caractéristique \(\tau\) de cette évolution est donc : \(\tau=0,5~\mbox{s}\).
Méthode : Méthode des tangentes
Nous raisonnons dans le cas où :
On sait que la grandeur étudiée suit une loi exponentielle décroissante (ou peut être modélisée par une exponentielle)
Et que l'évolution converge vers une valeur finie
Dans ce cas, pour déterminer le temps caractéristique d'évolution il faut :
Identifier l'asymptote aux temps longs (la droite horizontale vers laquelle la courbe temps)
Tracer la tangente à l'origine
Relever l'abscisse du point d'intersection entre la tangente et l'asymptote.
Attention : Attention aux dimensions
En sciences vous pouvez trouver ces évolutions décrites par le temps caractéristique (homogène donc à un temps) ou bien par une constante homogène à l'inverse d'un temps. C'est le cas par exemple lors d'une décroissance radioactive : \(N(t)=N_0\text{e}^{-\lambda t}\). Dans ce cas, l'abscisse du point d'intersection entre la tangente et l'asymptote vaut \(\dfrac 1\lambda\).