Déterminer le temps caractéristique d'une évolution exponentielle (méthode des 63 %)
Exemple : La charge d'un condensateur
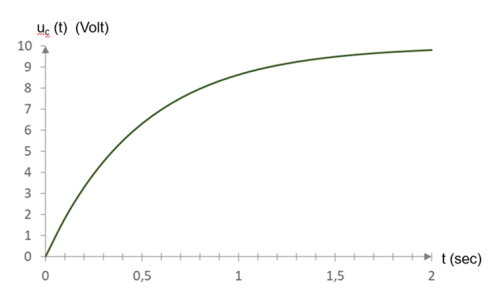
L'évolution temporelle de la tension \(u_{C}\) (unité : volt V) aux bornes d'un condensateur de capacité \(C\) lors de sa charge par un échelon de tension de valeur \( U_{0}=10~\mbox{V}\) dans un circuit RC est donnée sur le graphe ci-dessous (en vert).
L'équation horaire de \(u_{C}\) est du type : \(u_{C}(t) = U_{0} \times \left(1-\text{e}^{-\frac{t}{\tau}}\right)\)
\(\tau\) est la constante de temps (unité: seconde s).
Calculer la valeur de \(\tau\) .
Explication :
Lors d'une évolution exponentielle croissante de la forme :
\(u_{C}(t) = U_{0} \times \left(1-\text{e}^{-\frac{t}{\tau}}\right)\), la valeur du temps caractéristique correspond au temps pour lequel la tension aux bornes du condensateur vaut 63% de la valeur maximale \(u_{C max}\) de \(u_{C}(t)\).
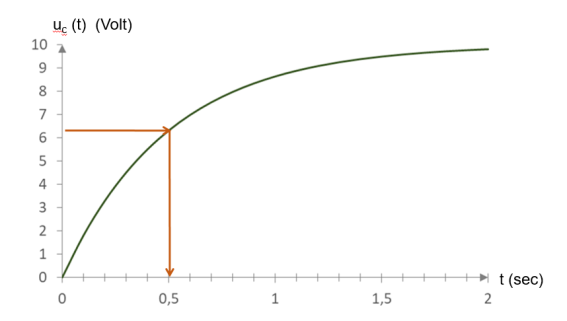
Lecture graphique :
Dans ce cas, \(u_{C max} = U_{0} = 10 \) V = asymptote au temps long
63% de \(u_{C max} =6,3~\mbox{V}=u_{C}(\tau)\)
Le temps caractéristique \(\tau\) de cette évolution est lu directement sur l'axe des abscisses donc : \(\tau=0,5 ~\mbox{s}\).
Méthode : Méthode de lecture sur graphe
Nous raisonnons dans le cas où :
On sait que la grandeur étudiée suit une loi exponentielle croissante de la forme \(u_{C}(t) = U_{0} \times (1-e^{-\frac{t}{\tau}})\)
On sait que la valeur maximale de \(u_{C}(t)\) au temps long vaut \(U_{max} = U_{0}\)
On démontre que pour \(t=\tau\), \(u_{C}(\tau) = U_{0} \times (1-e^{-\frac{\tau}{\tau}}) = U_{0} \times (1-e^{-1}) = 0,63 \times U_{0}\)
Dans ce cas, pour déterminer le temps caractéristique d'évolution il faut :
Calculer 63% de \(u_{C max}\)
Chercher la valeur de l'abscisse \(t=\tau\) correspondant :
\( u_{C}(\tau)=0,63\times U_{C max} = 0,63 \times U_{0}\)
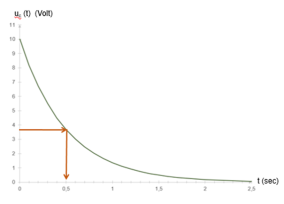
Attention : Attention à la décroissance exponentielle
Si le condensateur de capacité C se décharge dans un circuit RC, l'évolution temporelle de la tension \(u_{C}\) (unité : volt V) aux bornes du condensateur est donnée sur le graphe ci-dessous (en vert).
L'équation horaire de \(u_{C}\) est du type : \(u_{C}(t) = U_{0} \times (e^{-\frac{t}{\tau}})\)
Dans ce cas, la valeur de \(t=\tau\) correspond à l'abscisse pour laquelle on a :
\( u_{C}(\tau)=0,37 \times U_{C max} = 0,37 \times U_{0}\)