Réaliser une conversion simple
Exemple : De l'unité de base vers le multiple
Des éoliennes produisent une énergie E =\(1,6\times10^7\mbox{ W.h}\)
Calculer cette énergie en MW.h
Explication :
On exprime l'unité de départ (W.h) en fonction de l'unité d'arrivée : MW.h
\(1 \mbox{ W.h} = \dfrac{1}{10^{6}}\mbox{ MW.h}\)
On remplace dans l'expression l'unité de départ par l'unité d'arrivée :
\(\mbox{E}=1,6×10^7\mbox{ W.h}=1,6×10^7×10^{-6}\mbox{ MW.h}\)
On calcule le produit de puissances de 10 :
\(\mbox{E}=1,6×10^{7-6} =1,6×10^{1} \mbox{ MW.h}\)
Exemple : De l'unité de base vers le multiple
Des éoliennes produisent une énergie E =\(1,6\times10^7\mbox{ W.h}\)
Calculer cette énergie en MW.h.
Explication :
On exprime l'unité de départ (W.h) en fonction de l'unité d'arrivée : MW.h
\(1 \mbox{ W.h} = \dfrac{1}{10^{6}}\mbox{ MW.h}\)
On remplace dans l'expression l'unité de départ par l'unité d'arrivée :
\(\mbox{E}=1,6×10^7\mbox{ W.h}=1,6×10^7×10^{-6}\mbox{ MW.h}\)
On calcule le produit de puissances de 10 :
\(\mbox{E}=1,6×10^{7-6} =1,6×10^{1} \mbox{ MW.h}\)
Exemple : D'un sous-multiple à un autre sous-multiple
Calculer cette longueur d'onde en nm.
Explication :
On exprime l'unité de départ (mm) en fonction de l'unité d'arrivée : nm
Un millimètre (1 mm = 10-3 m) est 106 fois plus grand qu'un nanomètre
(1 nm = 10-9 m) donc : \(1 \mbox{ mm} = 10^{6}\mbox{ nm}\)
On remplace dans l'expression l'unité de départ par l'unité d'arrivée :
\(\lambda = 6,33×10^{-4}\mbox{ mm}=6,33×10^{-4}\times 10^{6} \mbox{ nm}\)
On calcule le produit de puissances de 10 :
\(\lambda =6,33×10^{-4+6}=6,33×10^{2} \mbox{ nm}\)
Méthode : Utiliser le tableau des multiples et sous multiples
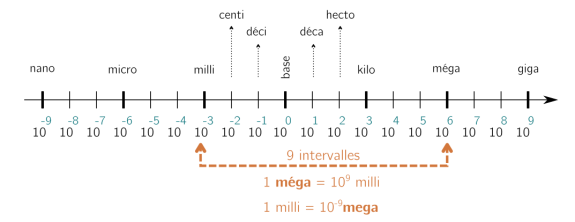
Repérer l'unité de départ et l'unité d'arrivée et les positionner sur l'axe des puissances
Compter le nombre de puissances qui les séparent
Choisir le signe de la puissance
Attention :
Il faut être vigilant au sens dans lequel s'effectue la conversion :
Un micromètre (\(10^{-6}\) m) est mille fois plus grand qu'un nanomètre (\(10^{-9}\) m), donc le coefficient de proportionnalité est plus grand que 1, l'exposant est positif :
1 \(\mu\)m = \(10^3\) nm
À l'inverse un nanomètre est mille fois plus petit qu'un micromètre, donc le coefficient de proportionnalité est plus petit que 1, l'exposant est négatif :
1 nm = \(10^{-3}\) \(\mu\)m
Rappel : Multiples et sous multiples
Chaque unité multiple et chaque unité sous-multiple est associée à un préfixe (micro, centi, déci, déca, kilo, giga, etc).
Chaque préfixe est associé à une puissance de 10.
Vers une unité plus petite : exposant positif
Exemples :
\(1\ \mbox{kg}=10^3\ \mbox g\).
\(1\ \mbox{A}=10^{3}\ \mbox {mA}\).
Vers une unité plus grande : exposant négatif
Exemples :
\(1\ \mbox{L}=10^{-2}\ \mbox{hL}\).
\(1\ \mbox{nm}=10^{-9}\ \mbox m\).