Sommer des vecteurs
Exemple : Somme de 3 vecteurs
Un solide est soumis à trois forces \(\overrightarrow{P}, \overrightarrow{F}\) et \(\overrightarrow{T}\). Dans la base \(\left(\overrightarrow {u_x}, \overrightarrow {u_y}\right)\) ces forces sont modélisés par les vecteurs : \(\overrightarrow {P} = 2a \overrightarrow {u_y}\), \( \overrightarrow {F} = -2\overrightarrow {u_x} + 3\overrightarrow {u_y}\) et \(\overrightarrow {T} = -a\overrightarrow {u_x} + b\overrightarrow {u_y}\) avec \(a\) et \(b\) deux nombres réels.
Donner l'expression du vecteur \(\overrightarrow{F_{tot}}=\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}\) .
Explication :
On écrit la somme de vecteurs en utilisant la décomposition dans la base \(\left(\overrightarrow {u_x}, \overrightarrow {u_y}\right)\) :
\(\overrightarrow{F_{tot}}=2a \overrightarrow {u_y}+-2\overrightarrow {u_x} + 3\overrightarrow {u_y}+-a\overrightarrow {u_x} + b\overrightarrow {u_y}\)
On regroupe ensemble les termes portés par le même vecteur de base :
\(\overrightarrow{F_{tot}}=(-2-a)\overrightarrow {u_x} + (2a+3+b) \overrightarrow {u_y} \)
Si on souhaite utiliser l'écriture en colonne, alors on reporte les expressions de chaque composantes : \(\overrightarrow{F_{tot}} \mbox{ } \begin{pmatrix}-2+-a\\2a+3+b \end{pmatrix}\)
Méthode : Calculer une somme ou une différence de vecteurs à l'aide des composantes dans une base orthonormée
Déterminer les composantes de chaque vecteur dans la base \((\overrightarrow {u_x}, \overrightarrow {u_y})\)
Réaliser la somme ou la différence de vecteurs en écrivant chaque vecteur en fonction des vecteurs de base
Regrouper les termes en facteur du même vecteur de base
Attention : La norme de la somme n'est pas égale à la somme des normes
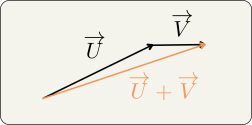
La norme d'une somme de \(\left\|\overrightarrow U+\overrightarrow V \right\|\) n'est pas égale à la somme d'une norme de vecteurs \(\left\|\overrightarrow U \right\|+\left\|\overrightarrow V \right\|\) comme on peut le voir sur le schéma ci-dessous.
Remarque : Écriture avec les vecteurs de base ou écriture en colonne ?
L'écriture avec les vecteurs de base aide à comprendre ce que l'on fait et évite de nombreuses erreurs, en particulier lorsque l'on travaille dans plusieurs bases dans un même exercice (mécanique).
L'écriture avec les vecteurs colonnes est plus efficace quand on est expert(e) pour mener les calculs lorsque l'on reste toujours dans la même base.