Utiliser les fonctions réciproques
Exemple : Exprimer v_E en fonction des autres grandeurs du problème à partir de la relation f_R = \dfrac{v_{son}}{v_{son} - v_E} \times f_E.
Exprimer \(v_E\) en fonction des autres grandeurs du problème à partir de la relation \(f_R = \dfrac{v_{son}}{v_{son} - v_E} \times f_E\).
Explication :
On repère quelle est la grandeur à isoler en la surlignant sur la copie : ici \(v_E\) est au dénominateur à droite \(f_R = \dfrac{v_{son}}{v_{son} - \textcolor{red}{v_E}} \times f_E\)
On se ramène à une équation en ligne en multipliant par \((v_{son} - v_E) \) donc :
\(f_R \times {(v_{son} - \textcolor{red}{v_E})}= v_{son} \times f_E\)
On isole la grandeur recherchée :
On développe : \(f_R v_{son} - f_R \textcolor{red}{v_E}= {v_{son}} f_E\)
On isole le terme contenant \(v_E\) en ajoutant \(-f_R v_{son} \) de part et d'autre du signe égal : \( - f_R \textcolor{red}{v_E}= {v_{son}} f_E - f_R v_{son}\)
On isole \(v_E\) en divisant l'expression par le préfacteur \("- f_R"\) et on obtient : \(\textcolor{red}{v_E}=\dfrac{v_{son} (f_E-f_R)}{-f_R}\)
On simplifie : \(\textcolor{red}{v_E}=v_{son}\left(1-\dfrac{f_E}{f_R}\right)\)
Méthode : Exprimer une grandeur à partir d'une relation quelconque
On identifie la grandeur recherchée qui joue le rôle de l'inconnue \(x\) en mathématiques
Si l'inconnue est présente au dénominateur : on se ramène à une équation en ligne
Si l'inconnue n'est présente qu'une fois mais "dans" une fonction :
On utilise les procédés réciproques pour progressivement isoler la grandeur recherchée
Les procédés réciproques
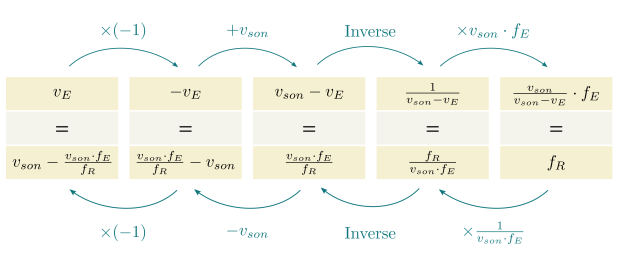
Une méthode qui marche souvent pour trouver comment isoler une grandeur dans une expression compliquée, c'est de recourir aux procédés réciproques. L'idée est de construire étape par étape l'expression de départ à partir de la grandeur à isoler ; et ensuite, de suivre les étapes dans l'ordre inverse en utilisant les procédés réciproques.
À la fin, il ne faut pas oublier de simplifier l'expression obtenue. Dans le cas de l'exemple illustré : \(v_E=v_{son}-\dfrac{v_{son}f_E}{f_R}=v_{son}\left(1-\dfrac{f_E}{f_R}\right)\)
Rappel : Les procédés réciproques
Procédé | Procédé réciproque |
Ajouter | Soustraire |
Multiplier par ... | Diviser par ... |
Élever au carré | Prendre la racine carrée |
Prendre l'inverse de | Prendre l'inverse de |
Prendre le logarithme népérien de ... | Prendre l'exponentielle de ... |
Prendre le logarithme décimal de ... | Prendre la puissance de 10 de ... |
Prendre le sin , le cos , la tan de ... | Prendre arcsin , arccos , arctan de ... |
Procédé réciproque | Procédé |
Attention aux domaines de définition des fonctions correspondantes. Quand plusieurs valeurs sont possibles il faut résoudre l'équation et pas juste appliquer les procédés réciproques.
Attention : Isoler n'est pas équivalent à résoudre une équation
Lorsque l'on manipule les fonctions trigonométriques et la fonction racine carrée, il faut vérifier :
Que la solution existe
Si il en existe plusieurs