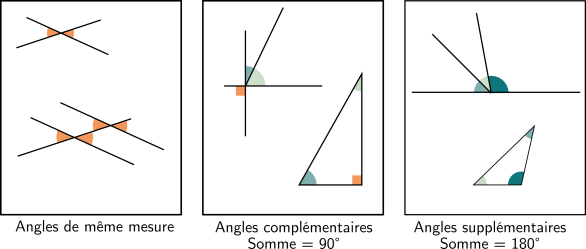Déterminer un angle à partir de droites parallèles
Exemple : Trouver un angle particulier
Trouver la valeur de l'angle (non orienté) \(h\) en fonction de \(\alpha\).

Explication :
On commence par identifier les relations entre les angles : angles de même mesure, complémentaires et supplémentaires
On code de la même manière les angles de même mesure.

On trouve un chemin pour aller de l'angle \(\alpha\) à l'angle \(h\)
\(\alpha+\textcolor{red}{a}= 90\mbox{°}\) : angles aigus du triangle rectangle
\(\textcolor{red}{a}=\textcolor{blue}{e}\) : angles opposés par le sommet
\(\textcolor{blue}{e}+\textcolor{magenta}{i}=90 \mbox{°}\) : angles aigus du triangle rectangle
\(\textcolor{magenta}{i}=h\) : angles opposés au sommet
On substitue les grandeurs : \(\alpha+90\mbox{°}-\mbox{i}=90\mbox{°} \Longrightarrow \alpha -i=0 \Longrightarrow \alpha=i\)
Méthode : Trouver un angle particulier en utilisant les relations entre angles
Poser le problème en repérant :
L'angle que l'on cherche à exprimer en fonction d'autres angles
Les angles connus, ou qui sont des paramètres du problème
Les figures particulières (droites parallèles, perpendiculaires et triangles rectangles) pour repérer les angles :
De même mesure (deux droites parallèles coupées par une sécante)
Complémentaires (composent un angle droit, 2 angles aigus d'un triangle rectangle)
Supplémentaires (composent un angle plat, 3 angles d'un triangle quelconque)
Rechercher un chemin entre l'angle (ou les angles) connu(s) et l'angle inconnu.
Exprimer ensuite successivement les expressions pour aller de l'angle connu à l'angle inconnu.
Résoudre le système d'équations
Méthode : Système d'équations
Lorsqu'il n'est pas simple (ou pas possible) de trouver un chemin pour aller d'un angle connu à l'angle que l'on recherche, on construit un système d'équations. Il faut alors autant d'équations indépendantes que d'angles utilisés pour que le système ait une solution.
Rappel : Les angles particuliers
Angles complémentaires ( leur somme vaut 90°) : découpent un angle droit, ou les deux angles aigus du triangle rectangle
Angles supplémentaires ( leur somme vaut 180°) : découpent un angle plat, 3 angles d'un triangle