Utiliser les relations de trigonométrie
Exemple : Trigonométrie simple
Une route a une pente indiquée de 10%.
On s'élève de 100 mètres lorsque l'on s'éloigne d'un kilomètre horizontalement (cf dessin).

Calculer l'angle entre la route et l'horizontale.
Explication :
Les deux côtés donnés sont les côtés opposé et adjacent de l'angle recherché. Il faut donc utiliser la tangente.
Calcul
On écrit la définition de la tangente (en mettant les données dans la même unité) : \(\tan(\alpha)=\dfrac{100 \mbox{ m}}{1000\mbox{ m}}\)
On prend ensuite l'arctangente pour isoler \(\alpha\): \(\alpha = \arctan(0,1)\)
On calcule en faisant attention au mode de la calculatrice : \(\alpha = 5,7 \mbox{°}\)
Exemple : Trigonométrie puis équation à résoudre
Un pendule est composé d'une masselotte suspendue à un fil de longueur \(\ell\) (voir figure ci-dessous)
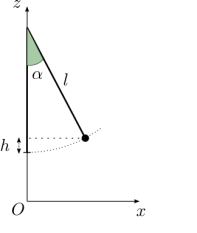
Donner l'expression littérale de la hauteur à laquelle la masselotte s'élève lorsque le pendule s'écarte d'un angle \(\alpha\) de la verticale.
Explication :
On travaille dans le triangle formé par le pendule par rapport à la barre verticale.
L'hypoténuse vaut alors \(\ell\) et le côté adjacent vaut \(\ell-h\).
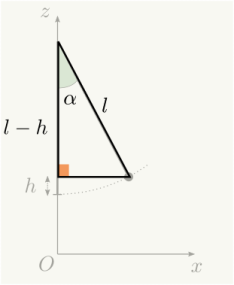
Calcul littéral : On cherche à isoler \(h\) dans \(\cos(\alpha)=\dfrac{\ell-h}{\ell}\)
On se ramène à une équation sans fraction en multipliant à gauche et à droit par \(l\) et on obtient : \(\ell \times\cos(\alpha)=\ell-h\)
Pour isoler \(h\) à gauche du signe égal on ajoute \(h-\ell\times\cos(\alpha)\) de chaque côté d'où : \(h=\ell-\ell\times\cos{\alpha}\)
On termine en factorisant \(\ell\) ce qui donne : \(h=\ell\times{(1-\cos(\alpha))}\)
Méthode : Utiliser la trigonométrie pour trouver une grandeur géométrique
Repérer et dessiner le triangle rectangle dans lequel on va travailler
Indiquer sur le triangle les lettres correspondant aux longueurs ou angles connus.
Surligner la grandeur inconnue et identifier dans le triangle deux autres grandeurs connues (longueur ou angle)
Écrire la relation de trigonométrie qui relie les deux grandeurs connues et la grandeur inconnue.
Isoler la grandeur inconnue
Réaliser l'application numérique
Attention : Degrés et radians
Il faut faire attention à bien vérifier le mode de la calculatrice (degré ou radians).
On passe des degrés aux radians en se souvenant que \(360 \mbox{°}=2\pi\) rad.
Remarque : Côté adjacent ou opposé
Il faut se rappeler que la notion de côté opposé à l'angle ou de côté adjacent à l'angle dépend de l'angle considéré dans le triangle rectangle comme illustré dans le dessin ci-dessous.

Remarque : D'abord le calcul littéral
Dans l'enseignement supérieur en physique-chimie, il faut toujours donner
Le résultat du calcul littéral (c'est à dire avec que des lettres, pas de valeur numérique)
Avant de réaliser l'application numérique (il n'y aura plus que des nombres et les unités)