Utiliser le théorème de Pythagore
Exemple : Trouver une longueur dans un triangle rectangle
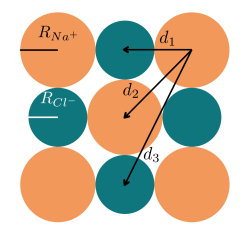
On considère une portion de cristal de chlorure de sodium. Les ions sodium sont représentés en orange clair sur le schéma et les ions chlorure en vert foncé.
Les ions sont assimilés à des sphères de rayons \(r_{Cl^-}= 181\) pm et \(r_{Na^+}=97\) pm.
Calculer la distance minimale \(d_2\) entre deux ions \(Na^+\).
Explication :
On reconnaît que la distance \(d_2\) que l'on cherche est l'hypoténuse d'un triangle rectangle isocèle dont les petits côtés ont une longueur \(d_1\).
La longueur \(d_1\) est égale à la somme du rayon d'un atome de chlore et du rayon d'un atome de sodium : \(d_1=r_{Cl^-} + r _{Na^+}\).
Schéma :
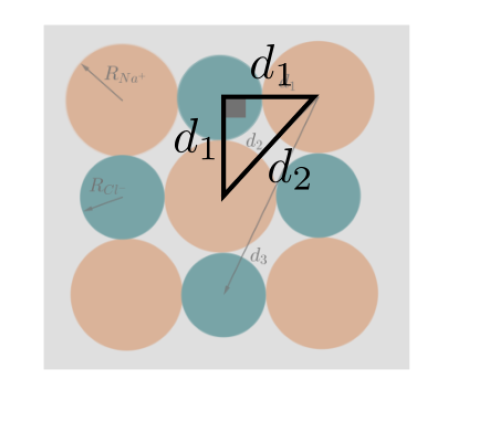
On dessine le triangle rectangle dans lequel on va appliquer le théorème de Pythagore
Calcul :
On applique le théorème de Pythagore dans le triangle rectangle : \(d_2~^2=d_1~^2+d_1~^2\).
On isole la grandeur recherchée
On additionne les termes en \(d_1~^2\) donc : \(d_2~^2=2d_1~^2\)
On prend la racine carrée (\(d_1\) est une distance donc forcément positif) :
\(d_2 = \sqrt{2d_1~^2}=d_1 \sqrt{2}\)
On remplace \(d_1\) par son expression en fonction des rayons des atomes :
\(d_2 =\sqrt{2}\times \left(r_{Cl^-} + r _{Na^+}\right)\).
Application numérique :
On remplace les données de l'énoncé par leur valeur en gardant l'unité :
\(d_2= \sqrt{2}\times (181 \mbox{ pm}+ 97\mbox{ pm})\).
On regroupe les nombres d'une part et les unités d'autre part :
\(d_2= \sqrt{2}\times (181+ 97)\mbox{ pm}= 393 \mbox{ pm}\)
Méthode : Théorème de Pythagore
Identifier et dessiner un triangle rectangle dont l'un des côtés est la grandeur inconnue et dont on puisse facilement connaître les longueurs des deux autres côtés.
Nommer les côtés avec des lettres si ce n'est pas déjà le cas.
Écrire le théorème de Pythagore avec les lettres
Isoler la grandeur recherchée
Réaliser l'application numérique
Attention : La racine carrée ne se distribue pas
\(\sqrt{a^2+b^2}\neq a+b\) comme vous pouvez le vérifier sur l'exemple \(\sqrt{3^2+4^2}=\sqrt{25}=5\)
mais \(3+4\neq 5\)
Remarque : D'abord le calcul littéral
Dans l'enseignement supérieur en physique-chimie, les enseignants attendent de vous que vous fassiez toujours le calcul littéral avant de faire l'application numérique.