Utiliser le théorème de Thalès
Exemple : Trouver une longueur avec le théorème de Thalès
Une personne observe la tour Eiffel de sa fenêtre. En tenant une règle à bout de bras, elle mesure une hauteur apparente de 30 cm. Les bras de cette personne mesurent environ 1 mètre de longueur et la tour Eiffel mesure elle 300 mètres de hauteur.
Calculer la distance entre cette personne et la tour Eiffel.
Explication :
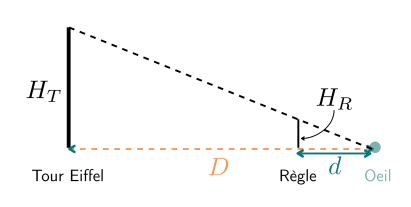
On fait un schéma de la situation et on reconnaît une situation avec des triangles semblables dans laquelle on peut appliquer le théorème de Thalès.
On nomme les longueurs en jeu :
\(H_T\) : Hauteur de la tour Eiffel
\(D\) : Distance œil - tour Eiffel (grandeur inconnue)
\(H_R\) : Longueur de la règle
\(d\) : Longueur du bras
Calcul littéral
On applique le théorème de Thalès : \(\dfrac{H_R}{H_T}=\dfrac{d}{D}\)
On isole la grandeur recherchée :
On applique l'égalité des produits en croix : \(DH_R=d H_T\)
On isole \(D\) en divisant par \(H_R\) alors : \(D=\dfrac{d H_T}{L_R}\)
Application numérique :
On remplace les données de l'énoncé par leurs valeurs avec les unités en mètres : \(D=\dfrac{300 \mbox{ m}\times 1 \mbox{ m}}{30\times10^{-2} \mbox{ m}}=1000\mbox{ m}\)
Méthode : Trouver une longueur en utilisant le théorème de Thalès
Repérer et dessiner les triangles dans lesquels on va travailler
Indiquer les lettres correspondant aux longueurs connues + longueur inconnue
Surligner la grandeur inconnue
Écrire le théorème de Thalès appliqué à la situation étudiée
Isoler la grandeur inconnue
Réaliser l'application numérique
Attention : En configuration papillon
Lorsque l'on écrit le théorème de Thalès, quelle que soit la configuration :
Les longueurs aux deux numérateurs appartiennent au même triangle.
Les longueurs aux deux dénominateurs appartiennent au même triangle.
Remarque : D'abord le calcul littéral
Dans l'enseignement supérieur en physique-chimie, les enseignants attendent de vous que vous fassiez toujours le calcul littéral avant de faire l'application numérique.