Déterminer une surface ou un volume
Exemple : Rechercher un volume
On cherche le volume de l'atmosphère terrestre en assimilant la Terre à une boule de rayon \(R_T=6400~\mbox{km}\). On fait l'hypothèse que l'atmosphère s'étend sur une hauteur \(h=30~\mbox{km}\).
Calculer le volume occupé par l'atmosphère terrestre.
Explication :
On calcule le volume recherché en faisant la différence entre le volume d'une boule de rayon \(R_T+h\) et le volume de la terre (boule de rayon \(R_T\)).
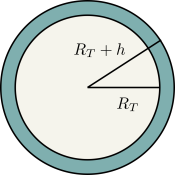
On calcule le volume \(V_1\) de la boule de rayon \(R_T+h ~\mbox{ :}~V_1=\dfrac43 \pi (R_T+h)^3\)
On calcule le volume \(V_2\) de la boule Terre de rayon \(R_T ~\mbox{ :}~V_2=\dfrac43 \pi R_T^3\)
On fait la différence entre les deux volumes : \(V_1-V_2=\dfrac43 \pi \left((R_T+h)^3-R_T^3\right)\)
Application numérique
On fait l'application numérique : \(V_1-V_2=\dfrac43 \pi \left(6430^3-6400^3\right)=1,55\times 10^{10}~\mbox{km}^3\)
Remarque :
On retrouve le fait que dans la limite où \(h\) est petit devant \(R_T\) la formule \([\rm Surface ]\times[hauteur]\) fonctionne.
Méthode : Détermination d'un volume ou d'une surface
Faire un schéma en indiquant les lettres représentant les grandeurs connues
Exprimer la grandeur recherchée en fonction d'une somme ou d'une différence de surfaces ou de volumes connus
Simplifier l'expression littérale si nécessaire
Réaliser l'application numérique
Remarque : Attention à l'homogénéité
L'expression d'une surface doit faire apparaître un produit de deux longueurs (ou une longueur au carré)
L'expression d'un volume doit faire apparaître un produit de trois longueurs (ou une longueur au cube)
Attention : Rayon et diamètre
Les formules des volumes sont données avec des rayons alors que dans la vie de tous les jours on a plutôt la donnée du diamètre.
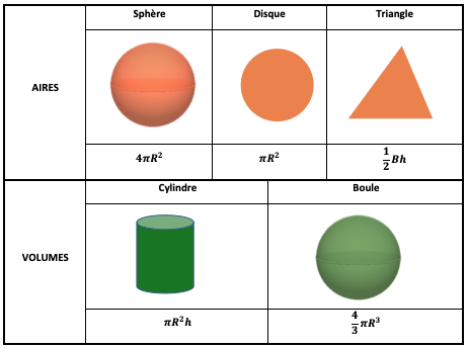
Rappel : Volumes et surfaces à connaître