Déterminer les composantes d'un vecteur par lecture graphique
Exemple : Vecteur position
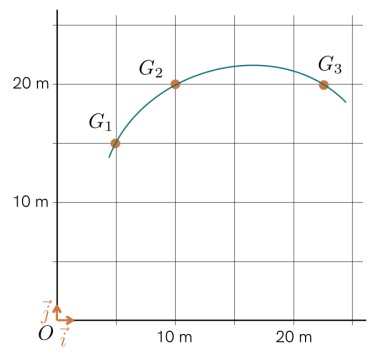
La position d'un point de l'extrémité d'un cerf-volant, noté G, est repérée à intervalle de temps réguliers dans le repère orthonormé (O ; \(\vec i\) , \(\vec j\)) lié au sol.
Écrire le vecteur \(\overrightarrow{OG_1}\) dans la base \(\left(\vec i , \vec j \right)\).
Explication :
Pour aller du point \(O\) au point \(G_1\) il faut se déplacer d'un carreau dans la direction de \(\vec i\) et de trois carreaux dans la direction de \(\vec j\).
Chaque carreau correspond à une distance de 5 mètres.
On a donc : \(\overrightarrow{OG_1}=5\times 1\vec i+3\times 5\vec j=5\vec i+15\vec j\)
On peut aussi écrire ce résultat en utilisant un vecteur colonne : \(\begin{pmatrix}5\\15\end{pmatrix}\)
Exemple : Vecteur position en coordonnées polaires
Dans un référentiel terrestre R supposé galiléen, on étudie le mouvement d'une bille roulant sans glisser sur un dôme hémisphérique (voir figure). La bille est en contact ponctuel avec le dôme au point A. On repère les composantes des vecteurs dans la base de vecteurs unitaires \(\left( \overrightarrow{e_\rho},\overrightarrow{e_\theta}\right)\).
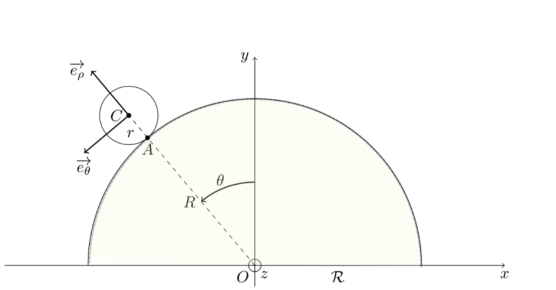
Déterminer les composantes du vecteur \(\overrightarrow{AC}\) dans la base \(\left( \overrightarrow{e_\rho},\overrightarrow{e_\theta}\right)\).
Explication :
Pour aller de A à C, il faut se déplacer de la distance \(r\) selon \(\overrightarrow{e_\rho}\) et de 0 selon \(\overrightarrow{e_\theta}\).
On a donc : \( \overrightarrow{AC}=r \overrightarrow{e_\rho}.\)
Pour exprimer le résultat en colonne on met donc les composantes de \(\overrightarrow{AC}\) dans un vecteur colonne : \(\overrightarrow{AC}\begin{pmatrix} r\\0\end{pmatrix}\)
Attention : Un vecteur n'est pas un nombre
À chaque fois que l'on écrit un vecteur, on doit utiliser une flèche. Un vecteur a plusieurs composantes, et ne peut jamais être égal à un nombre.
Lorsque l'on rédige, il faut toujours avoir vecteur(avec flèche)=vecteur(avec flèche), ou nombre(sans flèche)=nombre(sans flèche), mais jamais vecteur (avec flèche)=nombre (sans flèche).
Par exemple, on NE peut PAS écrire \(\overrightarrow{F} = 150 N\) mais il faut écrire \(\left\|\overrightarrow{F}\right\| = W= 150 N\)
Méthode :
Repérer les vecteurs de la base dans laquelle vous devez décomposer le vecteur
Positionner la base de vecteurs au départ du vecteur que vous avez à décomposer
Compter le nombre de fois que vous devez répéter chaque vecteur de base pour arriver au vecteur recherché
Écrire le résultat
Soit sous la forme vectorielle comme dans l'exemple : \(\overrightarrow{V}=3\overrightarrow{u_x}-2\overrightarrow{u_y}\)
Soit sous la forme matricielle comme dans l'exemple : \(\begin{pmatrix}3\\-2\end{pmatrix}\)
Rappel : Composantes (ou coordonnées) d'un vecteur
Un vecteur peut être écrit comme une somme des vecteurs d'une base orthonormée. Les vecteurs de la base orthonormée sont des vecteurs orthogonaux dont la norme vaut 1 : on parle de vecteurs unitaires.
En physique, les vecteurs unitaires sont souvent :
\(\overrightarrow{u_x}\) le vecteur unitaire selon la direction \((Ox)\)
\(\overrightarrow{u_y}\) le vecteur unitaire selon la direction \((Oy)\)
\(\overrightarrow{u_z}\) le vecteur unitaire selon la direction \((Oz)\)
En physique, on note en général \(V_x\) la composante du vecteur \(\overrightarrow V\) selon \(\overrightarrow{u_x}\).
On a donc : \(\overrightarrow{V}=V_x\overrightarrow{u_x}+V_y\overrightarrow{u_y}+V_z\overrightarrow{u_z}\)