Utiliser les caractéristiques d'un vecteur
Exemple : Vecteur position
Un ballon est lancé par un enfant, vers le haut.
Déterminer les caractéristiques du vecteur vitesse \(\overrightarrow{V}\) représenté ci-dessous :
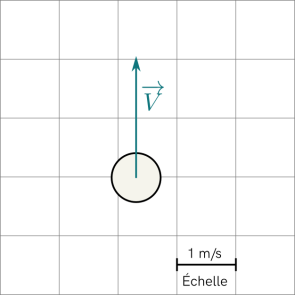
Explication :
Direction : le vecteur est vertical, sa direction est donc la verticale.
Sens : le vecteur pointe vers le haut, son sens est donc de bas en haut
Norme : la longueur du vecteur vitesse sur le schéma est de deux carreaux, avec l'échelle on a donc : \(\left\|\overrightarrow{V}\right\| = 2\) m/s.
Méthode :
On décrit un vecteur en donnant :
Sa direction (l'angle fait par la droite qui le porte et l'horizontale par exemple),
Son sens
Sa norme (sa "longueur" qui a la dimension de la grandeur décrite par le vecteur)
Remarque : Le vecteur ne modélise pas forcément un déplacement
En mathématiques, les vecteurs sont introduits pour décrire des déplacements. Dans ce cas, la longueur du vecteur s'exprime en mètres.
En physique, un vecteur peut modéliser une position (comme le vecteur \(\overrightarrow{OM}\)) et la norme de ce vecteur s'exprimera aussi en mètres. Mais un vecteur peut aussi modéliser une vitesse ou une force par exemple, et la norme de ce vecteur s'exprimera alors en mètres par seconde pour la vitesse ou bien en Newtons pour la force.
Remarque : Notations
En physique, les grandeurs sont décrites par des lettres.
La lettre avec une flèche dessus décrit une grandeur vectorielle comme le vecteur vitesse \(\overrightarrow V\) ou le vecteur position \(\overrightarrow{OM}\)
La lettre sans la flèche correspond à la norme du vecteur, c'est un nombre avec une unité. On parle alors de la norme de la vitesse, \(V\) en mètre par seconde, ou de la distance \(OM\) en mètres par exemple.