Projeter un vecteur
Exemple : Les composantes du poids
Un mobile de masse m glisse sur une pente faisant un angle \(\alpha\) avec l'horizontale
Exprimer les composantes du poids \(\overrightarrow{P}\) du mobile dans la base \(\left(\overrightarrow{u_{\parallel}},\overrightarrow{u_\perp}\right)\).
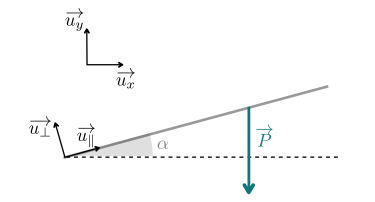
Explication :
Le vecteur \(\overrightarrow{P}\) n'est pas porté par l'un des deux vecteurs de base, il va donc falloir projeter ce vecteur. Pour projeter le vecteur \(\overrightarrow{P}\) on va construire un triangle rectangle dans lequel on pourra appliquer les formules de la trigonométrie.
1. Construire le triangle pour projeter
On dessine un triangle rectangle dont
L'hypoténuse est le vecteur \(\overrightarrow{P}\)
L'un des côtés est parallèle à la pente (et donc colinéaire au vecteur \(\overrightarrow{u_\parallel}\))
L'autre côté est perpendiculaire à la pente (et donc colinéaire au vecteur \(\overrightarrow{u_\perp}\))
On nomme les côtés du triangle
L'hypoténuse a pour norme \(\left\|\overrightarrow{P}\right\|=P\)
La valeur absolue de la composante sur \(\overrightarrow{u_{\parallel}}\) de \(P\) (\(|P_{\parallel}|\)) correspond au petit côté du triangle rectangle de la figure ci dessus.
La valeur absolue de la composante sur \(\overrightarrow{u_{\perp}}\) de \(P\) (\( |P_\perp|\)) correspond au grand côté du triangle rectangle de la figure ci dessus.
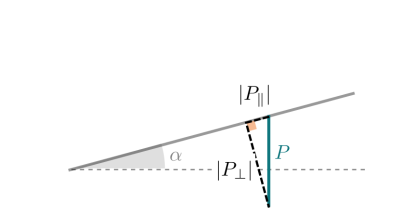
On a : \(\overrightarrow{P}=P_{\parallel}\overrightarrow{u_{\parallel}}+P_\perp \overrightarrow{u_\perp}\) et dans notre cas \(P_{\parallel}\) est négatif
2. Déterminer l'angle au sommet du triangle
On détermine les angles dans le triangle rectangle à partir des angles dessinés sur la figure et des angles particuliers :
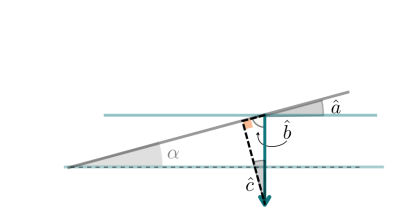
Angles particuliers :
Angles complémentaires (somme des angles dans un triangle rectangle) : \(\hat b=\dfrac{\pi}{2} -\alpha\)
Angles complémentaires (somme des angles dans un triangle rectangle): \(\hat c=\dfrac{\pi}{2}-\hat b\)
On a donc : \(\hat c=\alpha\)
On travaille donc dans le triangle rectangle suivant (on garde l'angle dont l'expression est la plus simple) :
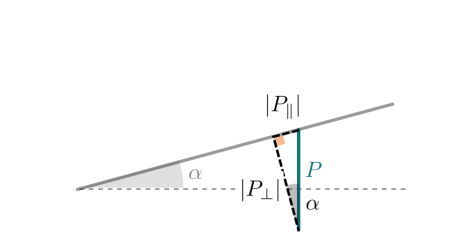
. Appliquer les formules de trigonométrie pour réaliser la projection
En utilisant les relations de trigonométrie, on obtient l'expression de \(P_{\parallel}\) et de \(P_\perp\) :
\(\cos(\alpha)=\dfrac{|P_\perp|}{P}\Longrightarrow |P_\perp|=P\cos(\alpha)\)
\(\sin(\alpha)=\dfrac{|P_{\parallel}|}{P}\Longrightarrow |P_{\parallel}|=P\sin(\alpha)\)
4. Choisir les signes
On choisit maintenant les signes :
La composante selon \(\overrightarrow{u_\perp}\) de \(\overrightarrow{P}\) est positive donc \(P_\perp= \textcolor{blue}{+} P\cos(\alpha)\)
La composante selon \(\overrightarrow{u_{\parallel}}\) de \(\overrightarrow{P}\) est négative donc \(P_{\parallel}= \textcolor{blue}{-}P\sin(\alpha)\)
5. Résultat
On écrit maintenant le vecteur en fonction des vecteurs de la base :
\(\overrightarrow{P}=-P\sin(\alpha)\overrightarrow{u_{\parallel}}+P\cos(\alpha)\overrightarrow{u_\perp}\)
Méthode : Projeter en utilisant la trigonométrie
Dessiner le triangle rectangle le plus pratique :
On commence par dessiner un triangle rectangle dont l'hypoténuse est le vecteur que l'on cherche à projeter et dont les deux autres côtés sont parallèles aux vecteurs de base.
Nommer les côtés de ce triangle avec les composantes du vecteur à projeter.
Déterminer les mesures des angles du triangle
On utilise les propriétés des angles particuliers pour trouver les angles de ce triangle rectangle.
Utiliser les relations de trigonométrie
On utilise les relations de trigonométrie pour trouver l'expression des composantes* en fonction de la norme du vecteur et de l'angle donné dans l'énoncé
Déterminer le signe de chaque composante
Écrire le résultat
On écrit le résultat \(\overrightarrow{V}=... \overrightarrow{u_{...}} + ... \overrightarrow{u_{...}} \) en faisant attention aux signes.
* en valeur absolue
Remarque : Autre méthode
Il est aussi possible de passer par le produit scalaire. En effet la composante de \(\overrightarrow V\) sur un axe de vecteur unitaire \(\overrightarrow u\) est \(\overrightarrow V \cdot \overrightarrow u =\left\|\overrightarrow V\right\|\times 1 \times \cos\left(\overrightarrow V, \overrightarrow u\right)\) mais déterminer l'angle \(\left(\overrightarrow V, \overrightarrow u\right)\) est parfois plus compliqué.