Sommer graphiquement des vecteurs
Exemple : Représentation d'une force résultante
Deux forces représentées dans le plan quadrillé peuvent agir sur un palet.

On soumet le palet à une force résultante \(\overrightarrow{R}\) telle que : \(\overrightarrow{R}=2\overrightarrow{F} + 3\overrightarrow{T}\).
Déterminer la représentation de la force résultante \(\overrightarrow{R}\).
Explication :
On dessine le vecteur \(\overrightarrow{F}\)
À son extrémité, on dessine une nouvelle fois le vecteur \(\overrightarrow F\) pour obtenir le vecteur : \(2\overrightarrow F\)
À l'extrémité, on dessine 3 fois de suite le vecteur \(\overrightarrow T\)
On dessine le vecteur \(\overrightarrow R=2\overrightarrow F+3\overrightarrow T\) qui relie l'origine du premier vecteur sommé à l'extrémité du dernier vecteur sommé
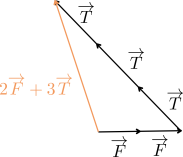
Remarque : On observe que la longueur du vecteur orange n'est pas égale à la longueur du trajet noir !
Méthode : Construire un vecteur somme
Pour déterminer un vecteur résultant de la somme (ou différence) de plusieurs vecteurs : \(\overrightarrow{U}+\overrightarrow{V} + \overrightarrow{W}\)
Dessiner le premier vecteur
Dessiner le second vecteur à l'extrémité du première vecteur (côté de la flèche)
Et ainsi de suite ...
Lorsque tous les vecteurs à sommer ont été dessinés, dessiner le "vecteur somme" qui relie l'origine du premier vecteur et l'extrémité du dernier vecteur.

Méthode : Construire la différence entre deux vecteurs
Le vecteur \(-\vec V\) a la même norme et la même direction que le vecteur \(\overrightarrow V\), mais son sens est différent. Pour construire la différence \(\overrightarrow W=\overrightarrow U-\overrightarrow V\) :
Dessiner le vecteur \(\overrightarrow U\)
Placer l'origine de l'opposé du vecteur \(\overrightarrow V\) à l'extrémité du vecteur \(\overrightarrow V\) \(~\)(côté flèche)
Le vecteur opposé est un vecteur qui a même direction et même norme, mais de sens opposé
Dessiner le vecteur différence qui relie l'origine du premier vecteur et l'extrémité du dernier vecteur.

Remarque : Vecteur nul
Lorsque l'extrémité du dernier vecteur additionné se positionne sur l'origine du premier vecteur, alors le vecteur somme est égal au vecteur nul : \(\overrightarrow 0\)
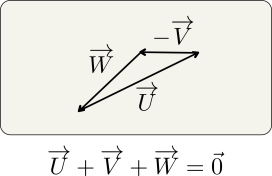
Conseil : Imaginez que vous vous déplacez
Pour additionner des vecteurs, imaginez que vous vous déplacez en suivant ces vecteurs. Pour faire la somme \(\overrightarrow U+\overrightarrow V\) vous vous déplacez d'abord en suivant la flèche \(\overrightarrow U\) puis ensuite, depuis là où vous êtes arrivé, vous vous déplacez en suivant la flèche \(\overrightarrow V\)