Trigonométrie - Niveau 2
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
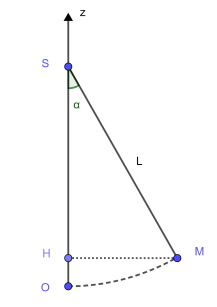
Un pendule de longueur \(L\) est accroché en \(S\). L'origine \(O\) du repère est prise à la position d'équilibre du pendule.
Quelle est la coordonnée du point \(M\) sur l'axe (\(Oz\)) quand le pendule est éloigné d'un angle \(\alpha\) de son axe ?
Correction
Explication Générale
Attention : L'axe (\(Oz\)) est orienté vers le haut et son origine prise en \(O\).
Raisonnement : On cherche la longueur \(HO\) (\(=z_M\)) qui est reliée à la longueur \(L\) du pendule par la relation \(HO=L-SH\).
Dans le triangle rectangle \(SHM\) on connaît l'angle \(\alpha\), la longueur \(L\) et on cherche \(SH\) : \(cos(\alpha) = \frac{SH}{SM} = \frac{SH}{L}\).
Calcul littéral : On isole \(SH\) en multipliant par \(L\) : \(SH=L\cos(\alpha)\).
Donc \(z_M = OH = L - L cos (\alpha) = L (1 - cos(\alpha))\).
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
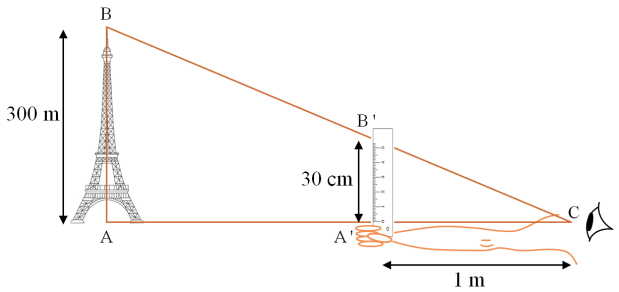
Une personne observe la tour Eiffel de sa fenêtre. En tenant une règle à bout de bras, elle mesure une hauteur apparente de 30 cm. Les bras de cette personne mesurent environ 1 mètre de longueur et la tour Eiffel mesure elle 300 mètres de hauteur. On cherche à déterminer la distance qui sépare cette personne de la tour Eiffel.
Quel outil va-t-on utiliser pour résoudre ce problème ?
Correction
Explication Générale
Raisonnement : Il est complètement équivalent d'appliquer le théorème de Thalès ou d'utiliser les formules trigonométriques sur les tangentes.
D'après l'énoncé et la formule ci-contre on sait que \(AB=300\mbox{ m}\), \(A'B'=30\mbox{ cm}\) et \(B'C=1\mbox{ m}\) et on cherche la distance à la tour Eiffel c'est-à-dire \(BC\).
Démonstration avec le théorème de Thalès :
Le théorème de Thalès nous donne la formule suivant : \(\frac{A'B'}{AB}=\frac{B'C}{BC}=\frac{A'C}{AC}\).
Comme les valeurs de \(AB\), \(A'B'\) et \(B'C\) sont connues on a l'égalité : \(BC=\frac{B'C\times{AB}}{A'B'}=\frac{1\times{300}}{30}\times\frac{1}{10^{-2}}\times\frac{\mbox{m}\times{\mbox{m}}}{\mbox{m}}=1000\mbox{ m}=1\mbox{ km}\).
Démonstration avec les formules de trigonométrie sur les tangentes :
Soit \(\alpha\) l'angle \(\widehat{ACB}\). D'après les règles de trigonométries appliquées aux tangentes, on a \(\tan{\alpha}=\frac{AB}{BC}\) mais aussi \(\tan{\alpha}=\frac{A'B'}{B'C}\).
Ainsi on obtient l'égalité \(\frac{AB}{BC}=\frac{A'B'}{B'C}\) \(\iff{}\) \(BC=\frac{B'C \times AB}{A'B'} =\frac{1\times{300}}{30}\times\frac{1}{10^{-2}}\times\frac{\mbox{m}\times{\mbox{m}}}{\mbox{m}}=1000 \mbox{ m}=1 \mbox{ km}\).
On obtient donc le même résultat quelle que soit la méthode utilisée.
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
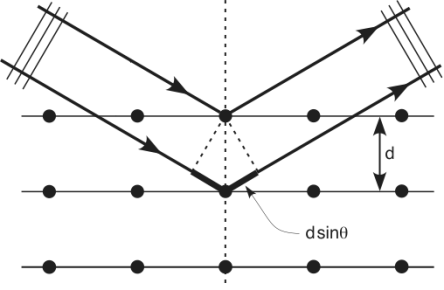
Pour connaître la distance \(d\) entre les atomes d'un cristal on utilise un réfractomètre : un faisceau lumineux est envoyé sur le cristal qui le diffracte.
La loi de Bragg donne la relation entre la distance inter-atomique, la longueur d'onde du faisceau lumineux et le demi-angle de déviation du faisceau lumineux : \(2d\sin{\theta}=n\lambda\).
On envoie un faisceau lumineux de longueur d'onde \( \lambda=520\) nm dans l'air (\(n=1\)) et on observe que le rayon diffracté fait un angle \(\frac{2\pi}{3}\) avec le rayon incident.
Que vaut la distance inter-atomique ?
Correction
Explication Générale
Raisonnement : D'après l'énoncé on sait qu'on doit utiliser la relation : \(2d\sin{\theta}=n\lambda\) pour isoler \(d\) qui a le rôle de variable.
On connait \(\theta = \frac{2\pi}{3}\), \(n=1\) et \(\lambda = 520\) nm qui ont le rôle de paramètres.
Calcul littéral : On isole \(d\) en divisant par son préfacteur \(2\sin{\theta}\) ce qui donne : \(d=\frac{n\lambda}{2\sin{\theta}}\).
Application numérique : \(d=\frac{520\mbox{ nm}}{2\sin({\frac{2\pi}{3}})}\approx 300\) nm.
Attention à bien configurer sa calculatrice en radian et non en degré.
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
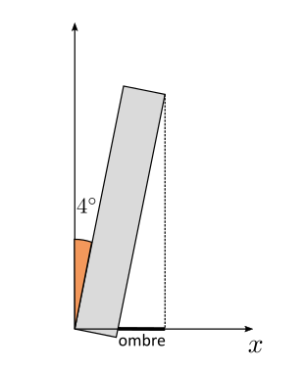
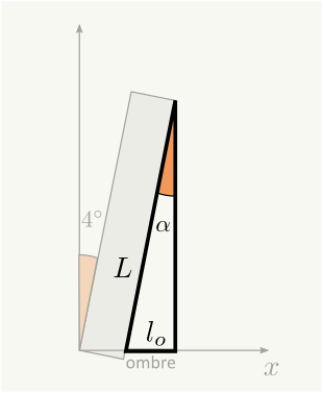
On modélise la tour de Pise par un rectangle de longueur 56 m qui penche avec un angle de 4°.
Quelle est la longueur de son ombre au sol lorsque le soleil est à la verticale ?
Correction
Explication Générale
Raisonnement : Appelons \(l_o\) la longueur de l'ombre. Cette grandeur inconnue correspond au petit côté d'un triangle rectangle dont on connaît la longueur d'un côté et d'un angle. On peut donc utiliser la relation de trigonométrie pour le sinus : \(\sin(\alpha)=\frac{l_o}{L}\).
Calcul littéral : On multiplie l'expression par \(L\) pour se ramener à une équation sans fraction : \(L\cdot \sin(\alpha) = l_o\).
Application numérique : \(l_o= \sin(4\mbox{°}) \times 56\mbox{ m}= 4 \mbox{ m}\).
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
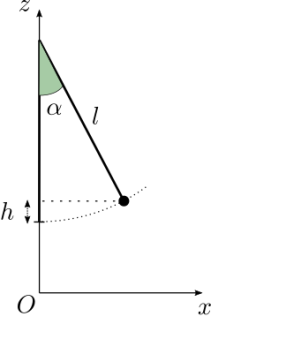
Un pendule est composé d'une masselotte suspendue à un fil de longueur \(l\) (voir figure ci-dessous).
Quelle est l'expression littérale de la hauteur à laquelle la masselotte s'élève lorsque le pendule s'écarte d'un angle \(\alpha\) de la verticale ?
Correction
Explication Générale
À savoir : \(\cos(\alpha)=\frac{\text{côté adjacent}}{\text{hypoténuse}}\), \(\sin(\alpha)=\frac{\text{côté opposé}}{\text{hypoténuse}}\) et \(\tan(\alpha)=\frac{\text{côté opposé}}{\text{côté adjacent}}\).
Raisonnement : On opère dans le triangle formé par le pendule par rapport à la barre verticale. L'hypoténuse vaut alors \(l\) et le côté adjacent vaut \(l-h\).
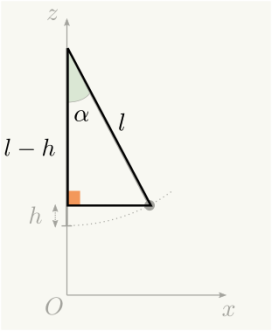
Calcul littéral : On cherche à isoler \(h\) dans \(\cos(\alpha)=\frac{l-h}{l}\).
On se ramène à une équation sans fraction en multipliant à gauche et à droite par \(l\) et on obtient \(l\cdot{\cos(\alpha)}=l-h\).
Pour isoler \(h\) à gauche du signe égal, on ajoute \(h-l\cdot\cos(\alpha)\) de chaque côté : \(h=l-l\cdot\cos{\alpha}\).
On termine en factorisant \(l\) : \(h=l\cdot{(1-\cos(\alpha))}\).
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
On considère que deux points sont aisément discernables à l'œil nu s'ils ont un diamètre apparent (angle \(\alpha\) sur le schéma) supérieur ou égal à \(3,5\cdot 10^{-4}\ \mbox{rad}\).
Une personne observe une feuille qui comporte deux traits parallèles. L'observateur est éloigné de \(5,0\ \mbox{m}\) de la feuille.
Quelle distance minimale doit-il y avoir entre les deux traits pour qu'ils soient distinguables à l'œil nu ?
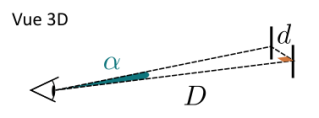
Correction
Explication Générale
Raisonnement : L’œil peut séparer les deux traits s'ils sont tels que \(\alpha>\alpha_{lim} =3,5\cdot 10^{-4}\mbox{ rad}\), c'est-à-dire s'ils sont éloignés d'une distance supérieure ou égale au cas limite ou \(\alpha=\alpha_{\mbox{lim}}\).
Calcul littéral : Dans le cas limite, \(\tan(\alpha_{\mbox{lim}})=\frac{d}{D}\) et donc en multipliant l'expression précédente par \(D\) on peut isoler \(d=\tan(\alpha_{\mbox{lim}})\cdot D\).
Application numérique : \(d=5\mbox{ m}\cdot \tan(3,5\cdot 10^{-4}\mbox{ rad})=1,75\cdot10^{-3} \mbox{ m}=1,75 \mbox{ mm}\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Quelles sont les affirmations juste sur le triangle dessiné ci-dessous ?
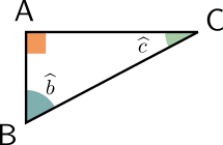
Correction
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Un pendule de longueur L est accroché en S.
On choisit un repère (Oxz) avec O l'origine du repère, l'axe des x orienté vers la droite de la figure et l'axe des z orienté vers le haut. Le point S a pour coordonnées (0,L).
Quelle est la coordonnée de M sur l'axe (0z) quand le pendule est éloigné d'un angle \(\alpha\) de son axe?
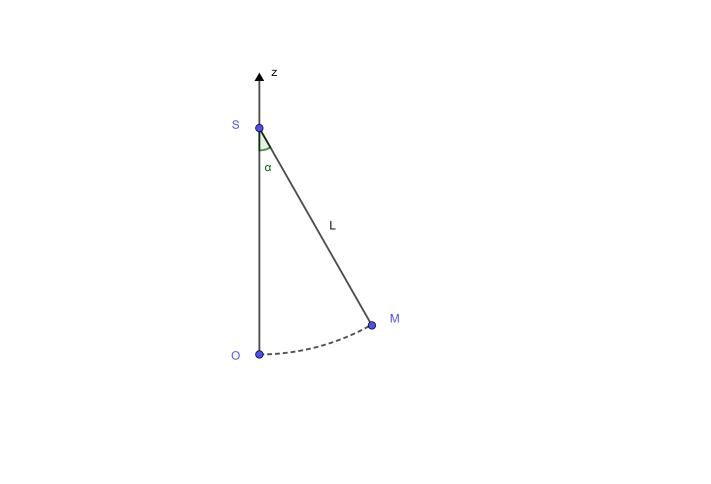
Correction
Explication Générale
Schéma : L'axe (Oz) est orienté vers le haut et son origine prise en S. Soit H le projeté de M sur l'axe (Oz). L'altitude du point M \(z_M\) est égale à OH.
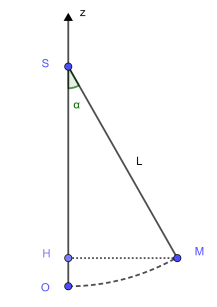
Calcul littéral :
On a par lecture du schéma :
OH = OS - SH
OS = L.
Détermination de SH :
Comme le triangle SHM est rectangle, on a : \(cos(\alpha) = \frac{SH}{SM} = \frac{SH}{L}\)
On a donc \(SH = L \cos(\alpha)\)
On réinjecte dans l'expression de OH : \(OH = L - L \cos(\alpha)\) et on factorise : \(OH=L(1-\cos\alpha)\)
On conclue : \(z_M =OH= L(1- \cos\alpha)\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Un pendule de longueur L est accroché en S.
Quelle est la coordonnée de M sur l'axe (0z) avec l'origine choisie en O quand le pendule est éloigné d'un angle \(\alpha\) de son axe?

Correction
Explication Générale
Raisonnement :
Soit H le projeté orthogonal de M sur l'axe vertical (Oz). On peut déterminer la distance HS dans le triangle SHM.
On remarque que OH = OS - HS .
L'axe (Oz) est orienté vers le haut avec son origine prise en O. L'altitude du point M \(z_M\) est alors positive et égale à +OH.
Calculs :
\(cos(\alpha) = \frac{HS}{MS} = \frac{HS}{L}\) dans le triangle rectangle SHM.
\(OS = L\) et \(HS = L \cos(\alpha)\)
On identifie: \(z_M = OH = L - L cos (\alpha) = L [1 - cos(\alpha)]\)

?Trouver l'expression d'une longueur
Énoncé
Un pendule de longueur L est accroché en S.
On choisit un repère (Sxz) avec S l'origine du repère, l'axe des x orienté vers la droite de la figure et l'axe des z orienté vers le haut.
Quelle est la coordonnée de M sur l'axe (Sz) quand le pendule est éloigné d'un angle \(\alpha\) de son axe?

Correction
Explication Générale
Raisonnement : L'axe (Oz) est orienté vers le haut et son origine est en S.
L'altitude du point M \(z_M\) est alors négative et égale à l'opposé de la distance SH

Calcul littéral :
Déterminons SH :
Dans le triangle rectangle SHM on a \(cos(\alpha) = \frac{SH}{SM} = \frac{SH}{L}\)
On a donc : \(SH=SM \cos \alpha\)
Or \(SM=L\), on a donc \(SH=L \cos \alpha\)
Déterminons \(z_M=-SH\) :
\(z_M = - L cos(\alpha)\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Un jeu de fête foraine consiste à envoyer le plus loin possible un objet de masse m sur un plan incliné.
Soit L la distance maximale parcourue par le mobile sur le plan incliné \(L=AB\).
On prendra pour origine des altitudes l'altitude du point A.
Exprimer l'altitude \(z_B\) de B en fonction de L et \(\alpha\), en prenant A comme origine de l'axe vertical (Oz).

Correction
Explication Générale
Raisonnement : On travaille dans un triangle rectangle d'hypoténuse L dans lequel on va utiliser les définitions des fonctions trigonométriques.
Schéma

Calcul littéral :
L'altitude du mobile en fin de montée est \(z_B - z_A\). Il s'agit de la longueur du côté opposé à l'angle alpha.
On peut utiliser la définition du sinus pour écrire : \(sin(\alpha) = \frac{z_B - z_A}{L} = \frac{z_B}{L}\)
Comme \(z_A = 0\), on a \(z_B = L sin (\alpha)\)