Angles et droites parallèles - Niveau 2
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
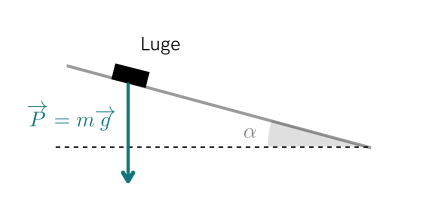
Une luge glisse entre \(A\) à \(B\) sur une pente qui fait un angle \(\alpha\) avec l'horizontale. Le travail du poids \(\vec{P}\) s'écrit \(W(\vec{P})=mg\cdot AB\cos(\vec{P} ;\vec{AB})\).
Que vaut l'angle entre le poids et le déplacement de la luge ?
Correction
Explication Générale
Raisonnement :
On commence par réaliser le schéma de la situation en représentant le vecteur déplacement \(\overrightarrow{AB}\)
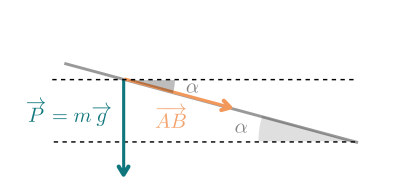
On dessine la droite parallèle à l'horizontale qui passe par l'origine des vecteurs poids et déplacement
Cette droite fait un angle \(\alpha\) avec la pente (angles alternes-internes)
L'angle entre \(\vec{P}\) et \(\vec{AB}\) mesure donc \(\frac{\pi}{2}-\alpha\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Un objet est tiré sur un plan incliné qui fait un angle \(\alpha\) avec l'horizontale entre deux points \(A\) à \(B\) non indiqués sur le schéma. Cet objet est soumis aux forces schématisées ci-dessous.
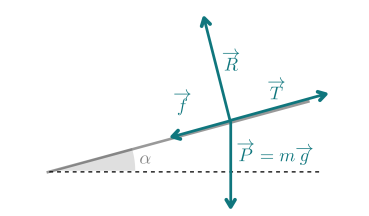
Le travail de la réaction du sol \(\vec{R}\) s'écrit \(W(\vec{R})=R \cdot \thinspace{AB}\cos(\vec{R} ;\vec{AB})\)
Que vaut l'angle entre la force de réaction du support et le déplacement \(\overrightarrow{AB}\) ?
Correction
Explication Générale
Schéma :
On dessine le schéma de la situation en représentant le vecteur \(\overrightarrow{AB}\)
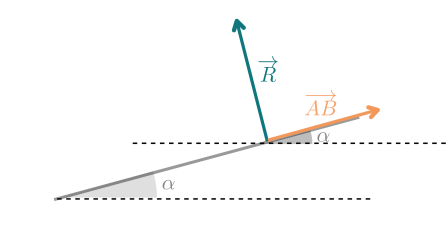
Le vecteur \(\vec{R}\) est orthogonal à \(\vec{AB}\), l'angle vaut donc 90° soit \(\frac{\pi}{2}\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Un objet est tiré sur un plan incliné qui fait un angle \(\alpha\) avec l'horizontale entre deux points \(A\) à \(B\) non indiqués sur le schéma. Cet objet est soumis aux forces schématisées ci-dessous

Le travail de la force de frottements \(\vec{f}\) s'écrit \(W(\vec{f})=f\cdot \thinspace{AB}\cos(\vec{f} ;\vec{AB})\)
Que vaut l'angle entre la force de frottement et le déplacement \(\overrightarrow{AB}\) ?
Correction
Explication Générale
Trouver l'angle
On commence par faire un schéma en dessinant le vecteur \(\overrightarrow{AB}\)
On constate que les vecteurs \(\vec{f}\) et \(\vec{AB}\) ont même direction mais sont de sens opposé
L'angle \((\vec{f} ;\vec{AB})\) est donc de 180° soit \(\pi\)
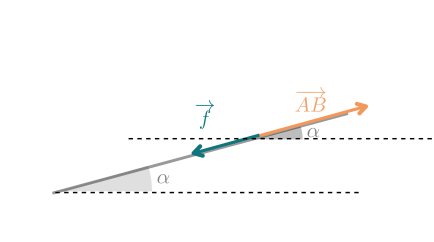
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Un objet est tiré sur un plan incliné qui fait un angle \(\alpha\) avec l'horizontale entre deux points \(A\) à \(B\) non indiqués sur le schéma. Cet objet est soumis aux forces schématisées ci-dessous.

Le travail du poids \(\vec{P}\) est donné par la relation \(W(\vec{P})=mg \cdot AB\cos(\vec{P} ;\vec{AB})\)
Quelle est l'expression du travail du poids en fonction de \(\alpha\) ?
Correction
Explication Générale
Raisonnement : On cherche d'abord l'angle entre \(\overrightarrow{P}\) et \(\overrightarrow{AB}\) et ensuite on calcule le produit scalaire.
Trouver l'angle entre \(\overrightarrow{P}\) et \(\overrightarrow{AB}\) :
Schéma :
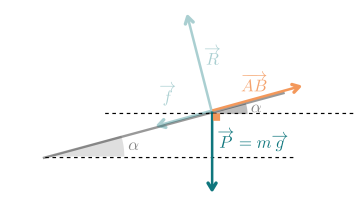
On trace un vecteur \(\overrightarrow{AB}\) qui part du même point que le vecteur poids \(\vec P\). Le vecteur \(\overrightarrow{AB}\) est porté par la droite parallèle au plan incliné.
On dessine la droite horizontale qui passe par le point A
La droite qui porte le plan incliné coupe deux droites parallèles : l'angle entre \(\overrightarrow{AB}\) et l'horizontale vaut donc \(\alpha\)
Le poids est porté par la verticale, l'angle entre \(\overrightarrow{AB}\) et le poids \(\overrightarrow{P}\) vaut donc \(\dfrac{\pi}{2}+\alpha\)
Écriture du produit scalaire
On écrit \(W(\vec{P})\) comme le produit scalaire du poids et du déplacement en utilisant la formule avec le cosinus : \(W(\vec{P})=mgAB\cos(\vec{P} ;\vec{AB})=mgAB\cos(\pi/2+\alpha)\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
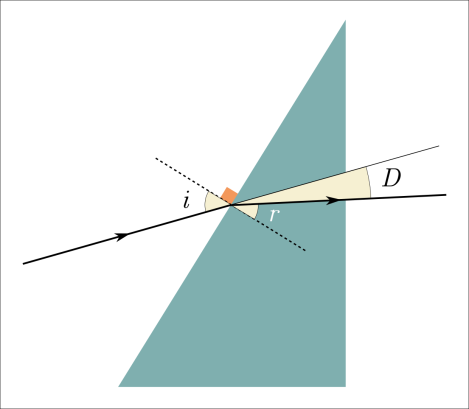
Quelle est l'expression de l'angle de déviation \(D\) en fonction des angles d'incidence \(i\) et de réfraction \(r\) ?
Correction
Explication Générale
Raisonnement :
Les angles \(i\) et \(D+r\) sont opposés par le sommet, ils sont donc égaux :
\(i=D+r\)
On isole ensuite \(D\) dans la relation précédente :
\(D+r=i \iff D=i-r\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
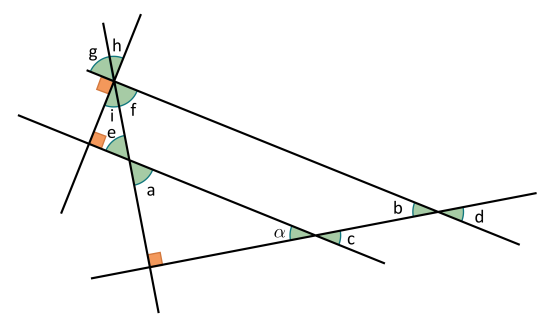
Quelle relation existe t-il entre l'angle (non orienté) \(h\) et \(\alpha\) ?
Correction
Explication Générale
Raisonnement :
On commence par repérer l'angle que l'on cherche à exprimer en fonction des autres angles : Ici on cherche à exprimer \(h\) en fonction de \(\alpha\)
On identifie les relations entre les angles :
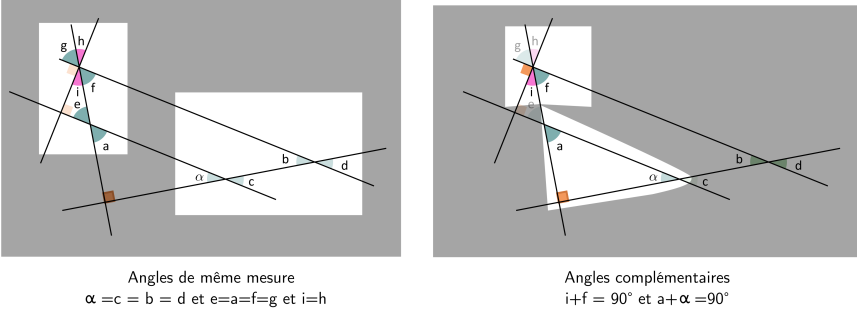
Angles de même mesure : \(\alpha=b=c=d\) ,\(e=a=f=g\) (deux droites parallèles coupées par une sécante), \(h=i\) (angles opposés par le sommet)
Angles complémentaires (somme vaut 90°) : \(i+f=90°\) (coupe un angle droit), \(a+\alpha=90°\) (deux angles aigus du triangle rectangle)
On trouve un chemin pour aller de l'angle \(h\) à \(\alpha\):
\(h=i\): angles opposés par le sommet
\(i+f=90°\) : coupe un angle droit
On isole \(f\) : \(f=\frac{\pi}{2}-i\)
\(a=f\) : deux droites parallèles coupées par une sécante
\(a+\alpha= 90°\): angles aigus du triangle rectangle
On remplace \(a\) par \(f\) : \(\frac{\pi}{2}-i+\alpha=\frac{\pi}{2}\)
On isole \(i\) : \(i=\alpha\)
On remplace \(i\) par \(h\) : \(h=\alpha\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Quelle relation existe t-il entre l'angle (non orienté) \(i\) et \(\alpha\) ?

Correction
Explication Générale
Raisonnement
On commence par repérer l'angle que l'on cherche à exprimer en fonction des autres angles : Ici on cherche à exprimer \(i\) en fonction de \(\alpha\)
On identifie les relations entre les angles :
Angles de même mesure : \(\alpha=b=c=d\) ,\(e=a=f=g\) (deux droites parallèles coupées par une sécante), \(h=i\) (angles opposés par le sommet)
Angles complémentaires (somme vaut 90°) : \(i+f=90°\) (coupe un angle droit), \(a+\alpha=90°\) (deux angles aigus du triangle rectangle)

On trouve un chemin pour aller de l'angle \(i\) à \(\alpha\):
\(i+f=90°\) : coupe un angle droit
On isole \(f\) : \(f=\frac{\pi}{2}-i\)
\(a=f\) : deux droites parallèles coupées par une sécante
\(a+\alpha= 90°\) : angle aigus du triangle rectange
On remplace \(a\) par \(f\) : \(\frac{\pi}{2}-i+\alpha=\frac{\pi}{2}\)
On isole \(i\) : \(i=\alpha\)
?Trouver l'expression d'un angle ou d'une longueur
Énoncé
Quelle relation existe t-il entre l'angle (non orienté) \(g\) et \(\alpha\) ?

Correction
Explication Générale
Raisonnement
On commence par repérer l'angle que l'on cherche à exprimer en fonction des autres angles : Ici on cherche à exprimer \(g\) en fonction de \(\alpha\)
On identifie les relations entre les angles :
Angles de même mesure : \(\alpha=b=c=d\) ,\(e=a=f=g\) (deux droites parallèles coupées par une sécante), \(h=i\) (angles opposés par le sommet)
Angles complémentaires (somme vaut 90°) : \(i+f=90°\) (coupe un angle droit), \(a+\alpha=90°\) (deux angles aigus du triangle rectangle)

On trouve un chemin pour aller de l'angle \(g\) à \(\alpha\):
\(g= a\) : deux droites coupées par une sécante
\(a+\alpha = 90°\) : angles aigus d'un triangle rectangle
On remplace \(a\) par \(g\) :
\(g +\alpha =90°\)
\(g = 90°-\alpha\)
Rappel : \(\frac{\pi}{2}=90°\)
On conclue : \(g=\frac{\pi}{2} - \alpha\)