Pourcentages - Niveau 1
?Représenter une situation
Dans une classe, il y a 25% de filles. Parmi les affirmations suivantes lesquelles sont exactes ?
Explication Générale
Dire que dans une classe il y a 25 pourcent de filles, cela signifie que s'il y avait 100 élèves, alors il y aurait 25 filles. Il s'agit d'une situation de proportionnalité.
?Représenter une situation
Dans une classe, il y a 25% de filles. Parmi les affirmations suivantes lesquelles sont exactes ?
Explication Générale
Raisonnement : Dire qu'il y a \(n\) pour cent de filles dans une classe c'est dire que le nombre de filles divisé par le nombre total d'élève est égal à \(\frac{n}{100}\). C'est-à-dire que \(\frac{N_{\mbox{filles}}}{N_{\mbox{filles}}+N_{\mbox{gars}}}=\frac{n}{100}\).
Application :
On a donc 25 filles pour 100 garçons (situation de proportionnalité).
\(25\%=\frac{25}{100}=\frac{25}{4\times 25}=\frac{1}{4}\) : un élève sur quatre est une fille.
?Représenter une situation
?Représenter une situation
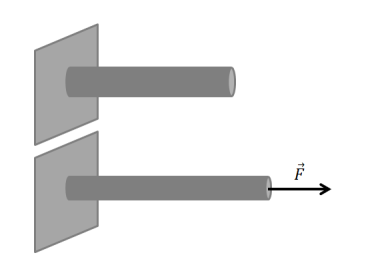
Une tige est soumise à une force axiale F. Son diamètre diminue. La déformation transversale de la tige est définie par son pourcentage de diminution.
Sachant que son diamètre passe de 1 cm à 0,83 cm
Quelle est la déformation transversale de la tige ?
Explication Générale
Méthode
La diminution de 1 à 0,83 correspond à une multiplication par un coefficient multiplicateur de \(\dfrac{0,83}{1}=0,83\)
Calcul
Donc ici ce coefficient donne une diminution de \(0,83=1-0,17=1-17 ~\%\), soit une déformation transversale de \(17 ~\%\)
?Représenter une situation
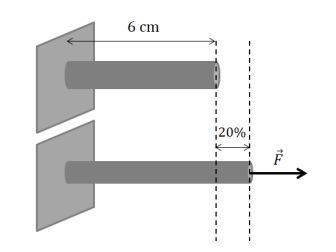
Une tige de longueur 6 cm est soumise à une force axiale F. La déformation longitudinale de la tige est définie par son pourcentage d'augmentation. Elle a une valeur de 20%.
Quelle est la valeur de la longueur de la tige en traction (cm)?
Explication Générale
Méthode
Soit L la longueur finale de la tige, l'augmentation de 6 à L correspond à une multiplication par un coefficient multiplicateur de \(\dfrac{L}{6}=1+20~\%=1+0,2=1,20\)
Calcul
Donc \(L = 6\times 1,2 = 7,2 cm\)
?Représenter une situation
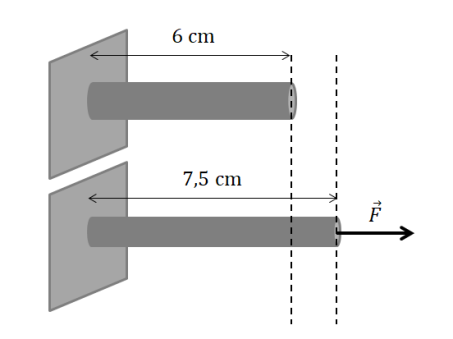
Une tige de longueur 6 cm est soumise à une force axiale F. Elle s'allonge pour mesurer en traction 7,5 cm. La déformation longitudinale de la tige est définie par son pourcentage d'augmentation.
Quelle est la déformation longitudinale de la tige ?
Explication Générale
Méthode
L'augmentation de 6 à 7,5 correspond à une multiplication par un coefficient multiplicateur de \(\dfrac{7,5}{6}=1,25\)
Calcul
Donc ici ce coefficient donne une augmentation de \(0,25=1+0,25=1+25 ~\%\), soit une déformation longitudinale de \(25 ~\%\)
?Représenter une situation
Une vitesse est passée de 240 km/h à 192 km/h. De quel pourcentage a-t-elle diminuée ?
Explication Générale
Méthode
La diminution de 240 à 192 correspond à une multiplication par un coefficient multiplicateur de \(\dfrac{192}{240}=0,8\)
Calcul
Donc ici ce coefficient donne une diminution de \(0,8=1-0,2=1-20 ~\%\), soit de 20 %
?Représenter une situation
Une vitesse est passée de 120 km/h à 180 km/h. De quel pourcentage a-t-elle augmentée ?
Explication Générale
Méthode
L'augmentation de 120 à 180 correspond à une multiplication par un coefficient multiplicateur de \(\dfrac{180}{120}=1,5\)
Calcul
Donc ici ce coefficient donne une augmentation de \(1,5=1+0,5=1+50 ~\%\), soit de 50 %
?Représenter une situation
Une vitesse de 320 km/h diminue de 40 %.
Quelle est la nouvelle vitesse ?
Explication Générale
Méthode
Une baisse de 40 % correspond à une multiplication par un coefficient multiplicateur de \(1-0,40=0,6\)
Calcul
Donc ici on a : \(320\times 0,6=192\)
?Représenter une situation
Une vitesse de 150 km/h augmente de 20 %.
Quelle est la nouvelle vitesse ?
Explication Générale
Méthode
Une augmentation de 20 % correspond à une multiplication par un coefficient multiplicateur de \(1+0,20=1,2\)
Calcul
Donc ici on a : \(150\times 1,2=180\)
?Représenter une situation
Le bore naturel est constitué de 2 isotopes naturels 10B et 11B dont les masses atomiques respectives sont 10,013 et 11,009 et les abondances respectives sont 18,929 % et 81,071 %.
Question : Calculer la masse atomique moyenne du bore.
Explication Générale
Raisonnement : La masse atomique moyenne est égale à la moyenne pondérée des masses atomiques de chaque isotope : \(M=p_1\times M_1+p_2\times M2\).
Aide : Ce problème a exactement la même structure que l'énoncé qui dirait : "Dans la seconde B il y a 46% de filles et 54% de garçons. La moyenne de la taille des filles est de 165 cm et celle des garçons est de 170 cm. Quelle est la moyenne de la taille des élèves de la classe ?"
Calcul : \(10,013\times \frac{18,929}{100} + 11,009\times \frac{81,071}{100} = 10,820\)