Produit scalaire - Niveau 1
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). On définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\).
Quels sont les vecteurs colinéaires ?
Correction
Explication Générale
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes. La première composante correspond à l'axe horizontal (axe des \(x\)) et la deuxième composante correspond à l'axe vertical (axe des \(y\)).
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux.
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux.
À savoir : deux vecteurs sont colinéaires quand ils sont dans la même direction, c'est-à-dire que les droites qui les portent sont parallèles.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). On définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\).
Quels sont les vecteurs verticaux ?
Correction
Explication Générale
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes. La première composante correspond à l'axe horizontal (axe des \(x\)) et la deuxième composante correspond à l'axe vertical (axe des \(y\)).
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux.
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). On définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\).
Quels sont les vecteurs horizontaux ?
Correction
Explication Générale
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes. La première composante correspond à l'axe horizontal (axe des \(x\)) et la deuxième composante correspond à l'axe vertical (axe des \(y\)).
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux.
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{v}\) et \(\overrightarrow{w}\) de coordonnées respectives \(\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}\) et \(\begin{pmatrix}w_x\\w_y\\w_z\end{pmatrix}\) dans \(\mathbb{R}^3\).
Quelles sont, par définition de la différence de deux vecteurs, les coordonnées du vecteur \(\overrightarrow{u}= \overrightarrow{v} - \overrightarrow{w}\) ?
Correction
Explication Générale
Les coordonnées de \(\overrightarrow{u}=\overrightarrow{v}-\overrightarrow{w}\) sont donnés par : \(\begin{pmatrix}v_x - w_x\\v_y-w_y\\v_z - w_z\end{pmatrix}\).
Voir http://uel.unisciel.fr/physique/outils_nancy/outils_nancy_ch03/co/apprendre_02_01.html.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{v}\) et \(\overrightarrow{w}\) de coordonnées respectives \(\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}\) et \(\begin{pmatrix}w_x\\w_y\\w_z\end{pmatrix}\) dans \(R^3\).
Quelles sont, par définition, les coordonnées du vecteur \(\overrightarrow{u}= \overrightarrow{v} + \overrightarrow{w}\) ?
Correction
Explication Générale
À savoir : Les coordonnées de \(\overrightarrow{u}=\overrightarrow{v}+\overrightarrow{w}\) sont donnés par : \(\begin{pmatrix}v_x + w_x\\v_y+w_y\\v_z + w_z\end{pmatrix}\).
Voir Ressource Unisciel.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
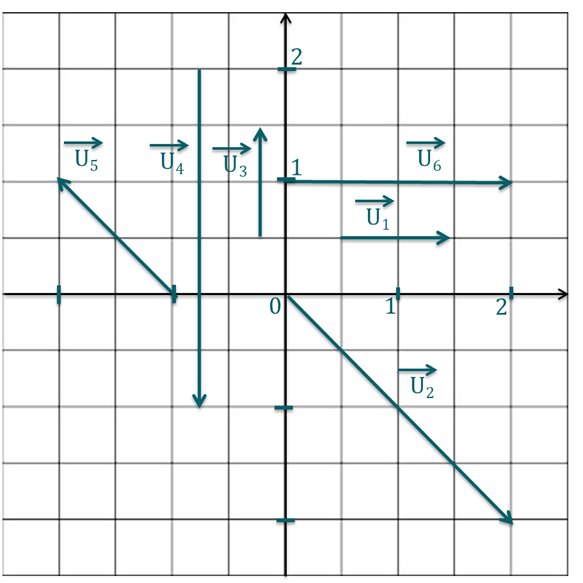
On considère les vecteurs représentés sur le schéma.
Quels sont les produits scalaires dont la valeur est égale à -2 ?
Correction
Explication Générale
On cherche un produit scalaire négatif : on cherche donc un produit scalaire entre deux vecteurs de sens opposés (l'un qui pointe vers la gauche, l'autre vers la droite). Les propositions possibles sont donc : \(\overrightarrow{U_5}\cdot \overrightarrow{U_6} \) et \( \overrightarrow{U_2}\cdot \overrightarrow{U_5}\).
On calcule alors les produits scalaires correspondants :
On lit sur le graphique les coordonnées des vecteurs :
\(\overrightarrow{U_2} \begin{pmatrix}2\\-2\end{pmatrix}\) ; \(\overrightarrow{U_5} \begin{pmatrix}-1\\1\end{pmatrix}\) ; \(\overrightarrow{U_6} \begin{pmatrix}2\\0\end{pmatrix}\).
Comme nous sommes dans un repère orthonormé on en déduit :
\(\overrightarrow{U_5}. \overrightarrow{U_6} = -1\times 2 + (1)\times 0 = -2\) ;
\(\overrightarrow{U_2}. \overrightarrow{U_5} = 2\times -1 + -2\times 1 = -4\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
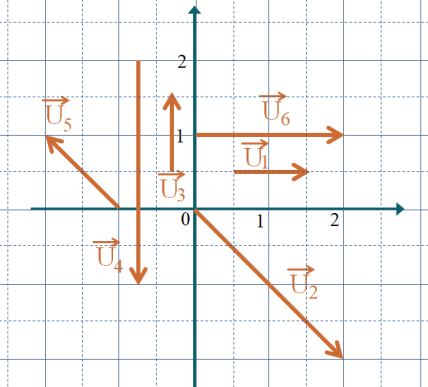
On considère les vecteurs représentés sur le schéma.
Quels sont les produits scalaires dont la valeur est égale à 2 ?
Correction
Explication Générale
On cherche un produit scalaire positif : il faut que les deux vecteurs impliqués soient dans le même sens.
Parmi les propositions, c'est donc uniquement possible pour : \( \overrightarrow{U_1}\cdot \overrightarrow{U_2}\) et \(\overrightarrow{U_1}\cdot \overrightarrow{U_6}\).
On calcule alors ces deux produits scalaires :
On lit sur le graphique les coordonnées suivantes :
\(\overrightarrow{U_1} \begin{pmatrix}1\\0\end{pmatrix}\) ; \(\overrightarrow{U_2} \begin{pmatrix}2\\-2\end{pmatrix}\) ; \(\overrightarrow{U_6} \begin{pmatrix}2\\0\end{pmatrix}\).
Comme nous sommes dans un repère orthonormé on en déduit :
\(\overrightarrow{U_1}. \overrightarrow{U_2} = 2\times 1 + (-2)\times 0 = 2\) ;
\(\overrightarrow{U_1}. \overrightarrow{U_6} = 1\times 2 + 0\times 0 = 2\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) dans l'espace, de coordonnées \(\begin{pmatrix}1\\-2\\4\end{pmatrix}\) et \(\begin{pmatrix}1\\-3\\0\end{pmatrix}\).
Que vaut le produit scalaire \(\overrightarrow{v_1}.\overrightarrow{v_2}\) ?
Correction
Explication Générale
On calcule le produit scalaire en effectuant \(\begin{pmatrix}1\\-2\\4\end{pmatrix}\cdot \begin{pmatrix}1\\-3\\0\end{pmatrix} = 1 \times 1 + (-2) \times (-3) + 4\times 0 = 1 + 6 = 7\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) dans l'espace, de coordonnées \(\begin{pmatrix}3\\-1\\2\end{pmatrix}\) et \(\begin{pmatrix}-1\\0\\3\end{pmatrix}\).
Que vaut le produit scalaire \(\overrightarrow{v_1}.\overrightarrow{v_2}\) ?
Correction
Explication Générale
On obtient le produit scalaire en effectuant \(\begin{pmatrix}3\\-1\\2\end{pmatrix}\cdot \begin{pmatrix}-1\\0\\3\end{pmatrix} = 3 \times (-1) + (-1) \times 0 + 2\times 3 = -3 + 6 = 3\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
\(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) sont deux vecteurs dans le plan tels que représentés sur le schéma suivant.
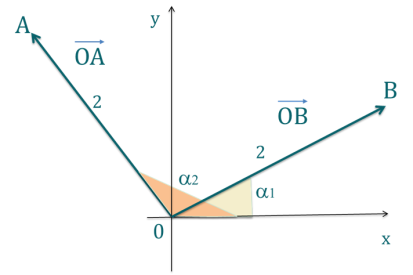
Que vaut leur produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) ?
Correction
Explication Générale
Le produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) est défini par \(\overrightarrow{OA} \cdot \overrightarrow{OB} = || \overrightarrow{OA} ||\cdot || \overrightarrow{OB}|| \cos( (\overrightarrow{OA},\overrightarrow{OB} )) = 2\times 2 \times \cos( \alpha_2 - \alpha_1)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
\(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) sont deux vecteurs dans le plan tels que représentés sur le schéma suivant.
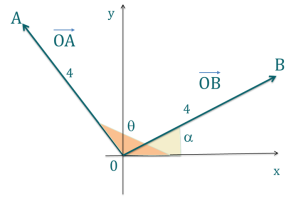
Que vaut leur produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) ?
Correction
Explication Générale
Le produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) est défini par \(\overrightarrow{OA} \cdot \overrightarrow{OB} = || \overrightarrow{OA} || \cdot || \overrightarrow{OB}|| \cos( (\overrightarrow{OA},\overrightarrow{OB} )) = 4\times 4 \times \cos( \theta - \alpha) = 16 \cos( \alpha - \theta)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit les vecteurs représentés ci-dessous.
Quel produit scalaire vaut 1 ?

Correction
Explication Générale
On cherche un produit scalaire positif : il faut que les deux vecteurs impliqués soient dans le même sens.
Parmi les propositions, c'est donc uniquement possible pour :\( \overrightarrow{u_2}\cdot\overrightarrow{u_4} \); \(\overrightarrow{u_1}\cdot\overrightarrow{u_6}\) et \(\overrightarrow{u_3}\cdot\overrightarrow{u_5}\).
On calcule alors ces trois produits scalaires :
\(\overrightarrow{u_2}\cdot\overrightarrow{u_4}= \begin{pmatrix}2\\-2\end{pmatrix} \cdot \begin{pmatrix}0\\-3\end{pmatrix}=2 \times 0 +(-2)\times (-3)=6\) ;
\(\overrightarrow{u_1}\cdot\overrightarrow{u_6} = \begin{pmatrix}1\\0\end{pmatrix} \cdot \begin{pmatrix}2\\0\end{pmatrix}=1 \times 2 +0\times 0=2\) ;
\(\overrightarrow{u_3}\cdot\overrightarrow{u_5}= \begin{pmatrix}0\\1\end{pmatrix} \cdot \begin{pmatrix}-1\\1\end{pmatrix}=0 \times (-1) +1\times 1=1\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit les vecteurs représentés ci-dessous.
Quel produit scalaire est égal à 2 ?

Correction
Explication Générale
On cherche un produit scalaire positif : il faut que les deux vecteurs impliqués soient dans le même sens.
Parmi les propositions, c'est donc uniquement possible pour : \( \overrightarrow{u_2}\cdot\overrightarrow{u_4} \); \(\overrightarrow{u_1}\cdot\overrightarrow{u_6}\) et \(\overrightarrow{u_3}\cdot\overrightarrow{u_5}\).
On calcule alors ces trois produits scalaires :
\(\overrightarrow{u_2}\cdot\overrightarrow{u_4}= \begin{pmatrix}2\\-2\end{pmatrix} \cdot \begin{pmatrix}0\\-3\end{pmatrix}=2 \times 0 +(-2)\times (-3)=6\) ;
\(\overrightarrow{u_1}\cdot\overrightarrow{u_6} = \begin{pmatrix}1\\0\end{pmatrix} \cdot \begin{pmatrix}2\\0\end{pmatrix}=1 \times 2 +0\times 0=2\) ;
\(\overrightarrow{u_3}\cdot\overrightarrow{u_5}= \begin{pmatrix}0\\1\end{pmatrix} \cdot \begin{pmatrix}-1\\1\end{pmatrix}=0 \times (-1) +1\times 1=1\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \( \overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) dans l'espace, de coordonnées respectives \((v_{1x}, v_{1,y}, v_{1,z})\) et \((v_{2x}, v_{2,y}, v_{2,z})\).
Comment s'exprime le produit scalaire \(\overrightarrow{v_1}.\overrightarrow{v_2}\) ?
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Comment s'exprime le produit scalaire entre \(\overrightarrow{u}\) et \( \overrightarrow{v}\) ? \(( \overrightarrow{u}, \overrightarrow{v})\) représente l'angle non-orienté entre \(\overrightarrow{u}\) et \(\overrightarrow{v}\) ?