Produit scalaire - Niveau 2
?Exprimer une grandeur à partir d'une relation vectorielle
On peut modéliser les actions agissant sur un avion qui se pose sur le pont d'un porte-avion par 3 forces :
son poids \(\overrightarrow{P}\) ;
la réaction normale de la piste \(\overrightarrow{N}\) ;
la force exercée par le filin sur la crosse d’appontage : \(\overrightarrow{R}\).
La position de l'avion au cours du temps est repérée par sa position \(\overrightarrow{OX(t)}\).
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\)., l'expression de ces vecteurs est :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX(t)}=\begin{pmatrix} x(t)\\0\end{pmatrix}\).
Quels sont les produits scalaires nuls ?
Explication Générale
À savoir : Le produit scalaire de deux vecteurs orthogonaux est nul.
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux.
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux.
Le produit scalaire de deux vecteurs horizontaux, ou de deux vecteurs verticaux sera différent de zéro et le produit scalaire d'un vecteur horizontal et d'un vecteur vertical sera nul.
?Exprimer une grandeur à partir d'une relation vectorielle
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). on définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\).
Sans faire de calcul, quels sont les produits scalaires non nuls ?
Explication Générale
À savoir : Le produit scalaire de deux vecteurs orthogonaux est nul.
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux.
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux.
Le produit scalaire de deux vecteurs horizontaux, ou de deux vecteurs verticaux sera différent de zéro et le produit scalaire d'un vecteur horizontal et d'un vecteur vertical sera nul.
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{l}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{l}\).
On se place dans un plan muni d'un repère \((O,\overrightarrow{i}, \overrightarrow{j})\). On considère une balle de masse m en chute libre soumise à son poids de 5 N représenté par \(\overrightarrow{P}\) et à une force de frottement de l'air d'intensité 0,01 N représentée par \(\overrightarrow{f}\).
Calculer le travail de la force du poids lors de la chute de la bille sur une hauteur de 100 m.
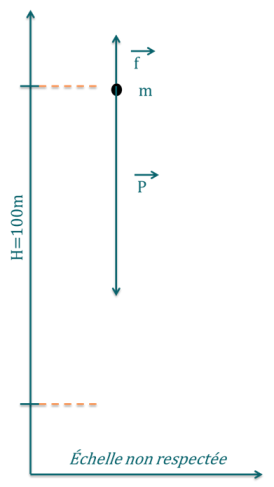
Explication Générale
\(\overrightarrow{P}\) et \(\overrightarrow{l}\) sont de même direction et de même sens. L'angle qui les relie vaut donc 0°.
Leur produit scalaire vaut \(\overrightarrow{P}\) .\( \overrightarrow{l} = || \overrightarrow{P} ||\) . \(|| \overrightarrow{l} || \cos(0\mbox{°}) = || \overrightarrow{P} ||\) .\( || \overrightarrow{l} || = 5 * 100\mbox{ J} = 500\mbox{ J}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{l}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{l}\).
On se place dans un plan muni d'un repère \((O,\overrightarrow{i}, \overrightarrow{j})\). On considère une balle de masse m en chute libre soumise à son poids de 10 N représenté par \(\overrightarrow{P}\) et à une force de frottement de l'air d'intensité 0,02 N représentée par \(\overrightarrow{f}\).
Calculer le travail de la force de frottement lors de la chute de la bille sur une hauteur de 100 m.

Explication Générale
\(\overrightarrow{f}\) et \(\overrightarrow{P}\) sont de même direction et de sens opposés. L'angle qui les relie vaut donc 180°.
Leur produit scalaire vaut \(\overrightarrow{f}\). \( \overrightarrow{P} = || \overrightarrow{f} ||\) . \(|| \overrightarrow{P} || \cos(180\mbox{°}) = - || \overrightarrow{f} ||\) .\( || \overrightarrow{P} || = - 0,02 * 100\mbox{ J} = -2\mbox{ J}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force \(\overrightarrow{T}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{L}\) (en m) est égal au produit scalaire \(\overrightarrow{T} .\overrightarrow{L}\).
On étudie la force de traction \(\overrightarrow{T}\) subie par skieur qui subit un déplacement \(\overrightarrow{L}\).
Quelle est l'expression du travail \(W\) de cette force en fonction de \(\alpha\) et \(\theta\) ?
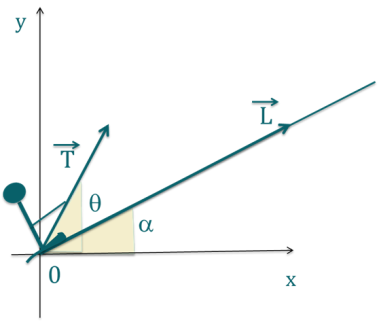
Explication Générale
La formule du produit scalaire fait intervenir l'angle entre les deux vecteurs, ici \(\theta- \alpha\).
On a donc \(\overrightarrow{T} . \overrightarrow{L} = ||\overrightarrow{T} || . || \overrightarrow{L} || \cos(\theta - \alpha)\).
De plus, \(\cos\) est paire donc \(\cos(\theta - \alpha) = \cos(\alpha - \theta)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{L}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{L}\).
On étudie la force \(\overrightarrow{F}\) subie par l'aile d'un avion qui subit un déplacement \(\overrightarrow{L}\).
Quelle est l'expression du travail \(W\) de cette force ?
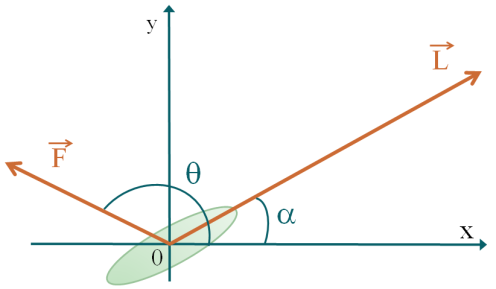
Explication Générale
La formule du produit scalaire fait intervenir l'angle entre les deux vecteurs, ici \(\theta- \alpha\).
On a donc \(\overrightarrow{F} . \overrightarrow{L} = ||\overrightarrow{F} || . || \overrightarrow{L} || \cos(\theta - \alpha)\).
De plus, \(\cos\) est paire donc \(\cos(\theta - \alpha) = \cos(\alpha - \theta)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force uniforme \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{l}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{l}\).
On se place dans un plan muni d'un repère \((O,\overrightarrow{i}, \overrightarrow{j})\). Le vecteur s'exprime sous la forme \(\overrightarrow{F} = F_X \overrightarrow{i} + F_Y \overrightarrow{j}\), avec \(F_X = -1\) N, \(F_y = -3\) N.
Le solide ponctuel M se déplace suivant un déplacement \(\overrightarrow{l} = l_x \overrightarrow{i} + l_y \overrightarrow{j}\), avec \(l_x = 4\) m et \(l_y = -2\) m.
Calculer le travail de \(\overrightarrow{F}\) appliquée au déplacement \(\overrightarrow{l}\) ?
Explication Générale
Le travail de \(\overrightarrow{F}\) appliqué au déplacement \(\overrightarrow{l}\) vaut \(\overrightarrow{F}.\overrightarrow{l}\).
\(\overrightarrow{F}.\overrightarrow{l} = F_x . l_x + F_y . l_y = -1*4+(-3)*(-2) = 2\) J.
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force uniforme \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{l}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{l}\).
On se place dans un plan muni d'un repère orthonormé \((O,\overrightarrow{i}, \overrightarrow{j})\). Le vecteur s'exprime sous la forme \(\overrightarrow{F} = F_X \overrightarrow{i} + F_Y \overrightarrow{j}\), avec \(F_X = 3\) N, \(F_y = -2\) N.
Le solide ponctuel M se déplace suivant un déplacement \(\overrightarrow{l} = l_x \overrightarrow{i} + l_y \overrightarrow{j}\), avec \(l_x = 1\) m et \(l_y = 2\) m.
Calculer le travail de \(\overrightarrow{F}\) appliquée au déplacement \(\overrightarrow{l}\).
Explication Générale
Le travail de \(\overrightarrow{F}\) appliqué au déplacement \(\overrightarrow{l}\) est défini par \(\overrightarrow{F}.\overrightarrow{l}\).
\(\overrightarrow{F}.\overrightarrow{l} = F_x . l_x + F_y . l_y = 3*1 + (-2)*2 = 3-4 = -1\) J.
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force uniforme \( \overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \( \overrightarrow{l}\) (en m) est égal au produit scalaire \( \overrightarrow{F} .\overrightarrow{l}\).
Calculer le travail d'une force de norme 3 N qui déplace son point d'application de 40 cm, l'angle entre \( \overrightarrow{F}\) et \(\overrightarrow{l}\) étant de 60°.
Explication Générale
\(\overrightarrow{F}.\overrightarrow{l} = || \overrightarrow{F}|| . || \overrightarrow{l} || \cos(120°) = 3*0,4*0,5 = 0,6J\)
?Exprimer une grandeur à partir d'une relation vectorielle
Le travail (en J) effectuée par une force uniforme \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M , lors d'un déplacement \( \overrightarrow{l}\) (en m) est égal au produit scalaire\( \overrightarrow{F} .\overrightarrow{l}.\)
Calculer le travail d'une force de norme 2 N qui déplace son point d'application de 30 cm, l'angle entre \( \overrightarrow{F}\) et \(\overrightarrow{l}\) étant de 120°.
Explication Générale
\(\overrightarrow{F}.\overrightarrow{l} = || \overrightarrow{F}|| . || \overrightarrow{l} || \cos(120°) = 2*0,3*(-0,5) = -0,3J\)
?Exprimer une grandeur à partir d'une relation vectorielle
Quelle doit être la norme du vecteur \(\overrightarrow{U}\) pour que le produit scalaire entre les deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) soit égal à 6 ?
Données : \(\cos(60°) = \frac{1}{2}\)
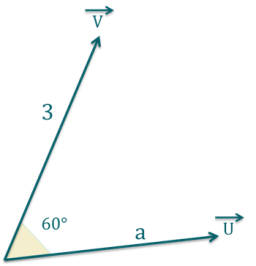
Explication Générale
Le produit scalaire de ces deux vecteurs vaut \(3* \cos(60) *a\) . Pour être égal à 6, il faut donc que \(a* \frac{1}{2} = 2\), soit \(a = 4\).
?Exprimer une grandeur à partir d'une relation vectorielle
Quelle doit être la norme du vecteur \(\overrightarrow{U}\) pour que le produit scalaire entre les deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) soit égal à 3 ?
Données : \(\cos(60°) = \frac{1}{2} \)

Explication Générale
Le produit scalaire de ces deux vecteurs vaut \( 3\times \cos(60) \times a\) . Pour être égal à 3, il faut donc que \(a\times \frac{1}{2} = 1\), soit \(a = 2\).
?Exprimer une grandeur à partir d'une relation vectorielle
Un hélicoptère peut se déplacer horizontalement ou verticalement dans un plan vertical. On note \(\overrightarrow{H}\) son déplacement vertical orienté vers le haut, \(\overrightarrow{B}\) son déplacement vertical orienté vers le bas, \(\overrightarrow{D}\) son déplacement horizontal orienté à droite et \(\overrightarrow{G}\) son déplacement horizontal orienté à gauche.
La gravitation exerce une force \(\overrightarrow{P}\) verticale orientée vers le bas. Le travail d'une force \(\overrightarrow{P}\) sur un trajet \(\overrightarrow{T}\) est donnée par le produit scalaire \(\overrightarrow{P}.\overrightarrow{T}\).
Dans quel(s) cas le travail de la force de gravité est-il strictement négatif ?
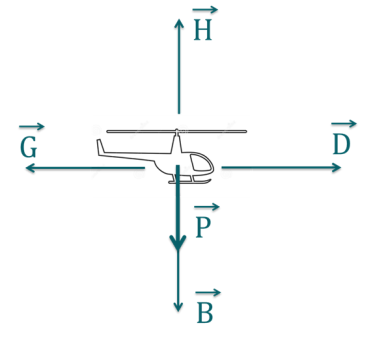
Explication Générale
Dans ce cas, la gravité exerce une force verticale vers le bas. Il faut donc que le déplacement ait une composante orientée vers le haut pour que le produit scalaire soit strictement négatif. Il faut donc que le déplacement s'effectue vers le haut.
?Exprimer une grandeur à partir d'une relation vectorielle
Un hélicoptère peut se déplacer horizontalement ou verticalement dans un plan vertical. On note \(\overrightarrow{H}\) son déplacement vertical orienté vers le haut, \(\overrightarrow{B}\) son déplacement vertical orienté vers le bas, \(\overrightarrow{D}\) son déplacement horizontal orienté à droite et \(\overrightarrow{G}\) son déplacement horizontal orienté à gauche.
La gravitation exerce une force \(\overrightarrow{P}\) verticale orientée vers le bas.
Le travail d'une force \(\overrightarrow{P}\) sur un trajet \(\overrightarrow{T}\) est donnée par le produit scalaire \(\overrightarrow{P}.\overrightarrow{T}\).
Dans quel(s) cas le travail de la force de gravité est-il strictement positif ?

Explication Générale
Dans ce cas, la gravité exerce une force verticale vers le bas. Il faut donc que le déplacement ait une composante orientée vers le bas pour que le produit scalaire soit strictement positif. Il faut donc que le déplacement s'effectue vers le bas.
?Exprimer une grandeur à partir d'une relation vectorielle
Un hélicoptère peut se déplacer horizontalement ou verticalement dans un plan vertical. On note \(\overrightarrow{H}\) son déplacement vertical orienté vers le haut, \(\overrightarrow{B}\) son déplacement vertical orienté vers le bas, \(\overrightarrow{D}\) son déplacement horizontal orienté à droite et \(\overrightarrow{G}\) son déplacement horizontal orienté à gauche.
La gravitation exerce une force \(\overrightarrow{P}\) verticale orientée vers le bas.
Le travail d'une force \(\overrightarrow{P}\) sur un trajet \(\overrightarrow{T}\) est donnée par le produit scalaire \(\overrightarrow{P}.\overrightarrow{T}\).
Dans quel(s) cas le travail de la force de gravité est-il nul ?

Explication Générale
Le produit scalaire de deux vecteurs est nul lorsque les deux vecteurs sont orthogonaux. Dans ce cas, la gravité exerce une force verticale vers le bas. Si le travail de la gravité pendant le déplacement est nul, c'est que le déplacement se fait de manière orthogonale à la force, c'est-à-dire horizontalement vers la droite ou vers la gauche.
?Exprimer une grandeur à partir d'une relation vectorielle
Soit une masse positionnée en \(A\) qui subit une force \(\overrightarrow{F}\) et qui se déplace de \(A\) vers \(B\).
Le travail d'une force \(\overrightarrow{F}\) sur un chemin (\(AB\)) est donné par la formule \(W = \overrightarrow{F}.\overrightarrow{AB}\).
Plusieurs déplacements sont possibles (vers le point \(B_1, B_2, B_3, B_4, B_5, B_6\) ou \(B_7\)) (cf schéma).
Pour quel(s) déplacement(s) le travail de la force\( \overrightarrow{F}\) sera-t-il le plus important ?

Explication Générale
Le travail est défini dans l'énoncé comme le produit scalaire entre le vecteur force \(\overrightarrow{F}\) et le vecteur déplacement \(overrightarrow{AB_i}\).
Quand \(\overrightarrow{F} \bot \overrightarrow{AB_i}\), leur produit scalaire est nul.
Quand l'angle entre \(\overrightarrow{F}\) et \(\overrightarrow{AB_i}\) est compris entre 90° et 180° : le produit scalaire est négatif, et donc plus petit qu'un produit scalaire positif.
\(\overrightarrow{AB_1}\) et \(\overrightarrow{AB_2}\) sont de même norme et font le même angle avec \( \overrightarrow{F}\), donc \(\overrightarrow{F}\).\(\overrightarrow{AB_1} = \overrightarrow{F}\).\(\overrightarrow{AB_7}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Les vecteurs représentés ci-dessous ont tous la même norme.
Parmi les produits scalaires suivants, lequel est le plus petit ?
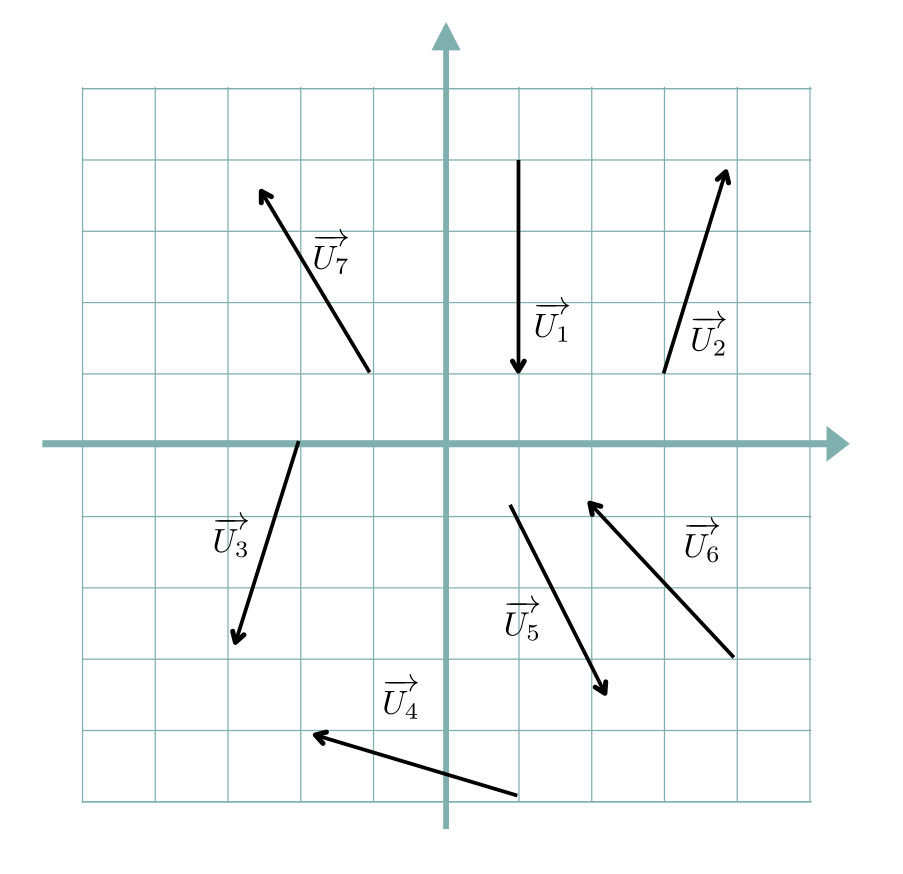
Explication Générale
Des propositions données, seuls \(\overrightarrow{U_1}.\overrightarrow{U_2}\) et \( \overrightarrow{U_1}.\overrightarrow{U_6}\) sont négatifs. Par contre, l'angle entre \( \overrightarrow(U_1)\) et \(\overrightarrow{U_2}\) est plus grand que celui entre \(\overrightarrow(U_1\)) et \(\overrightarrow{U_6}\). Donc \( \overrightarrow{U_1}.\overrightarrow{U_2} < \overrightarrow{U_1}.\overrightarrow{U_6}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Les vecteurs représentés ci-dessous ont tous la même norme.
Parmi les produits scalaires suivants, lequel est le plus grand ?
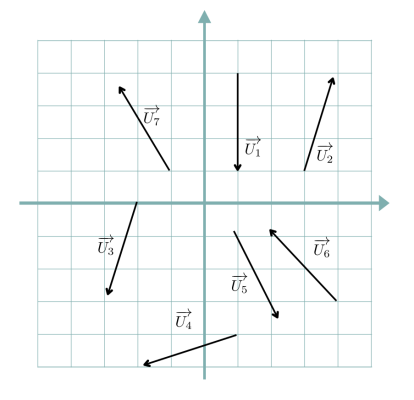
Explication Générale
Des propositions données, seuls \(\overrightarrow{U_1}.\overrightarrow{U_3}\),\( \overrightarrow{U_1}.\overrightarrow{U_5}\) sont positifs. Comme \(\overrightarrow{U_1}\) est vertical orienté dans le même sens que les deux vecteurs, il suffit de regarder la longueur de la cordonnée verticale. C'est donc \(\overrightarrow{U_1}.\overrightarrow{U_3}\) qui est le plus grand produit scalaire.
?Exprimer une grandeur à partir d'une relation vectorielle
Parmi les produits scalaires suivants, lesquels sont négatifs ?
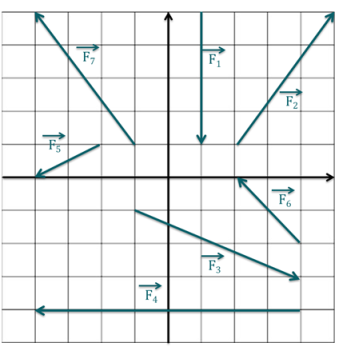
Explication Générale
À savoir : Pour que le produit scalaire entre deux vecteurs soit positif, il suffit que l'angle formé par les deux vecteurs à partir d'un même point d'application soit aigu (compris entre 0 et 90°). C'est-à-dire que les deux vecteurs pointent vers le même cadran, par exemple les deux vers "en haut, à droite".
Réciproquement, si l'angle entre les vecteurs est compris entre 90° et 180°, alors le produit scalaire sera négatif.
Cela se démontre à partir de la formule du produit scalaire : \(\overrightarrow{u}\cdot\overrightarrow{v}=||\overrightarrow{u}||\cdot||\overrightarrow{v}||\cdot\cos(\overrightarrow{u},\overrightarrow{v})\) où le cosinus est positif si l'angle est aigu (compris entre 0 et 90° en valeur absolue).
?Exprimer une grandeur à partir d'une relation vectorielle
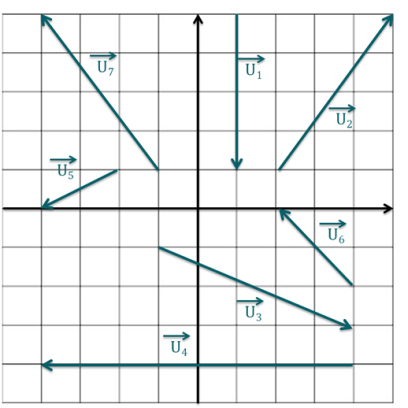
Soient les vecteurs représentés ci-dessous.
Parmi les produits scalaires suivants, lesquels sont négatifs ?
Explication Générale
À savoir : Pour que le produit scalaire entre deux vecteurs soit positif, il suffit que l'angle formé par les deux vecteurs à partir d'un même point d'application soit aigu (compris entre 0 et 90°). C'est-à-dire que les deux vecteurs pointent vers le même cadran, par exemple les deux vers "en haut, à droite".
Réciproquement, si l'angle entre les vecteurs est compris entre 90° et 180°, alors le produit scalaire sera négatif.
Cela se démontre à partir de la formule du produit scalaire : \(\overrightarrow{u}\cdot\overrightarrow{v}=||\overrightarrow{u}||\cdot||\overrightarrow{v}||\cdot\cos(\overrightarrow{u},\overrightarrow{v})\) où le cosinus est positif si l'angle est aigu (compris entre 0 et 90° en valeur absolue).
?Exprimer une grandeur à partir d'une relation vectorielle
Parmi les produits scalaires suivants, lesquels sont positifs ?

Explication Générale
À savoir : Pour que le produit scalaire entre deux vecteurs soit positif, il suffit que l'angle formé par les deux vecteurs à partir d'un même point d'application soit aigu (compris entre 0 et 90°). C'est-à-dire que les deux vecteurs pointent vers le même cadran, par exemple les deux vers "en haut, à droite".
Réciproquement, si l'angle entre les vecteurs est compris entre 90° et 180°, alors le produit scalaire sera négatif.
Cela se démontre à partir de la formule du produit scalaire : \(\overrightarrow{u}\cdot\overrightarrow{v}=||\overrightarrow{u}||\cdot||\overrightarrow{v}||\cdot\cos(\overrightarrow{u},\overrightarrow{v})\) où le cosinus est positif si l'angle est aigu (compris entre 0 et 90° en valeur absolue).
?Exprimer une grandeur à partir d'une relation vectorielle
Soient les vecteurs représentés ci-dessous. Ils ont tous la même norme.
Parmi les produits scalaires suivants, lequel(s) est (sont) le(s) plus grand(s) ?

Explication Générale
Comme les vecteurs ont la même norme, il suffit de comparer les angles entre les vecteurs. Le produit scalaire le plus élevé sera celui pour lequel l'angle est aigu (le cosinus sera strictement positif) et le plus petit possible (le cosinus sera le plus grand). L'angle entre \(\overrightarrow{U_1}\) et \(\overrightarrow{U_3}\) est le même que celui entre \(\overrightarrow{U_1}\) et \(\overrightarrow{U_5}\). Les deux réponses sont justes.
?Exprimer une grandeur à partir d'une relation vectorielle
On considère deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de norme non nulle. On appelle angle \(\alpha\) l'angle non orienté entre les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Dans quel(s) cas a-t-on le produit scalaire \(\overrightarrow{u}.\overrightarrow{v}\) égal à 0 ?
Explication Générale
Le produit scalaire \(\overrightarrow{u}.\overrightarrow{v}\) est donné par \(\overrightarrow{u}.\overrightarrow{v} ) = ||\overrightarrow{u}|| ||\overrightarrow{v} || \cos((\overrightarrow{u}, \overrightarrow{v})) \).
Comme \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont de norme non nulle, le seul cas où le produit scalaire s'annule est le cas où \(\cos((\overrightarrow{u}, \overrightarrow{v})) = 0\), c'est-à-dire le cas où les deux vecteurs sont orthogonaux.
?Exprimer une grandeur à partir d'une relation vectorielle
On considère deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) de norme non nulle.
Quelles propositions permettent de compléter de manière juste la phrase suivante "Un produit scalaire entre deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC} ...\)" ?
Explication Générale
Le produit scalaire \(\overrightarrow{u}. \overrightarrow{v} = ||\overrightarrow{u}||. ||\overrightarrow{v} ||. \cos(( \overrightarrow{u}, \overrightarrow{v}))\).
Le résultat est un nombre réel (appelé aussi “scalaire”) qui peut prendre des valeurs positives comme des valeurs négatives ou nulles.
?Exprimer une grandeur à partir d'une relation vectorielle
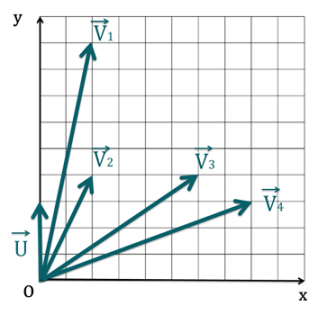
Soient les vecteurs représentés ci-dessous.
Sans faire de calcul, mais en raisonnant à partir de vos connaissances sur le produit scalaire, dire quels produits scalaires ont la même valeur.
Explication Générale
Comme tous les produits scalaires sont calculés par rapport à \(\overrightarrow{U}\), pour déterminer les valeurs des produits scalaires on s’intéresse à la valeur de \(||\overrightarrow{V_i}||.\cos (\overrightarrow{U}. \overrightarrow{V_i})\). Cette grandeur est obtenue en projetant le vecteur \(\overrightarrow{V_i}\) sur l'axe \(Oy\). Seuls les vecteurs \(\overrightarrow{V_2}\) et \(\overrightarrow{V_3}\) ont la même coordonnée selon \(Oy\).
?Exprimer une grandeur à partir d'une relation vectorielle
Soient les vecteurs représentés ci-dessous.
Sans faire de calcul, mais en raisonnant à partir de vos connaissances sur le produit scalaire, dire quels produits scalaires ont la même valeur.

Explication Générale
Comme tous les produits scalaires sont calculés par rapport à \(\overrightarrow{U}\), pour déterminer les valeurs des produits scalaires on s’intéresse à la valeur de \(||\overrightarrow{V_i}||.\cos (\overrightarrow{U}. \overrightarrow{V_i})\). Cette grandeur est la projection du vecteur \(\overrightarrow{V_i}\) sur l'axe \(Ox\).
Seuls les vecteurs \(\overrightarrow{V_2}\) et \(\overrightarrow{V_3}\) ont la même coordonnée selon \(Ox\).
?Exprimer une grandeur à partir d'une relation vectorielle
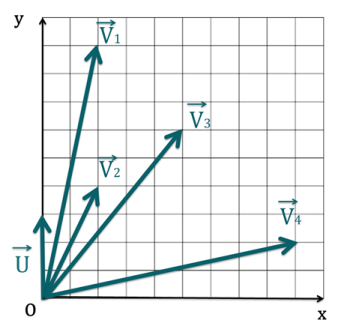
Soient les vecteurs représentés ci-dessous.
Sans faire de calcul, mais en raisonnant à partir de vos connaissances sur le produit scalaire, dire quel produit scalaire a la valeur la plus élevée dans la liste suivante.
Explication Générale
Tous les produits scalaires sont calculés avec \(\overrightarrow{U}\) qui est parallèle à l'axe des \(y\).
Pour déterminer le produit scalaire le plus élevé on compare les composantes selon y des vecteurs \(\overrightarrow{V_i}\).
Or on a \(V_{4y}<V_{2y}<V_{3y}<V_{1y}\). Donc, le plus grand produit scalaire est celui avec \(\overrightarrow{V_1}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Sans faire de calcul, quel produit scalaire a la valeur la plus élevée ?

Explication Générale
Tous les produits scalaires sont calculés avec \(\overrightarrow{U}\) qui est parallèle à l'axe des \(x\).
Pour déterminer le produit scalaire le plus élevé on compare les composantes selon \(x\) des vecteurs \(\overrightarrow{V_i}\).
Or on a \(V_{1x}<V_{2x}<V_{3x}<V_{4x}\). Donc, le plus grand produit scalaire est celui avec \(\overrightarrow{V_4}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Un objet est tiré sur un plan incliné qui fait un angle \(\alpha\) avec l'horizontale entre deux points \(A\) à \(B\) non indiqués sur le schéma. Cet objet est soumis aux forces schématisées ci-dessous.
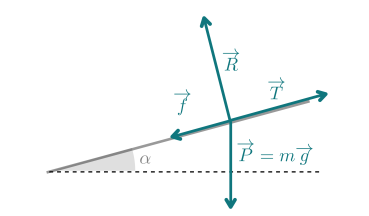
Le travail de la force de frottements \(\vec{f}\) s'écrit \(W(\vec{f})=f\cdot\thinspace{AB}\cos(\vec{f} ;\vec{AB})\)
Quelle est l'expression du travail des forces de frottement en fonction de l'angle \(\alpha\) ?
Explication Générale
Raisonnement : On recherche d'abord l'angle entre les vecteurs, ensuite on en calcule le cosinus.
Trouver l'angle
On commence par faire un schéma en dessinant le vecteur \(\overrightarrow{AB}\)
On constate que les vecteurs \(\vec{f}\) et \(\vec{AB}\) ont même direction mais sont de sens opposé
L'angle \((\vec{f} ;\vec{AB})\) est donc de 180° soit \(\pi\)

Calcul du produit scalaire :
On a donc : \(W(\vec{f})=f\cdot\thinspace{AB}\cos(\pi)\)
On calcule le cosinus en utilisant la valeur particulière \(\cos(\pi)=-1\) et on a : \(W(\vec{f})=-f\cdot\thinspace{AB}\)
?Exprimer une grandeur à partir d'une relation vectorielle
Un objet est tiré sur un plan incliné qui fait un angle \(\alpha\) avec l'horizontale entre deux points \(A\) à \(B\) non indiqués sur le schéma. Cet objet est soumis aux forces schématisées ci-dessous.

Le travail de la réaction du sol \(\vec{R}\) s'écrit \(W(\vec{R})=R \cdot\thinspace{AB}\cos(\vec{R} ;\vec{AB})\)
Que vaut le travail de la réaction du sol pendant le déplacement AB ?
Explication Générale
Schéma :
On dessine le schéma de la situation en représentant le vecteur \(\overrightarrow{AB}\)
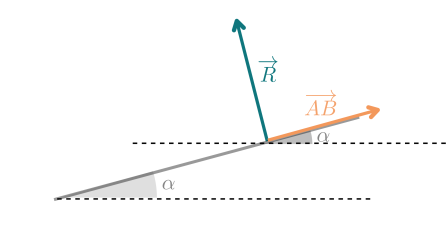
Raisonnement : le vecteur \(\vec{R}\) est orthogonal à \(\vec{AB}\), leur produit scalaire est donc nul.
Remarque : on peut aussi écrire la formule du produit scalaire pour arriver au même résultat : L'angle \((\vec{R} ;\vec{AB})\) est donc de 90° et \(W(\vec{R})=R\cdot\thinspace{AB}\cos(\pi)\)