Extremum - Niveau 2
?Exprimer une grandeur à partir d'une relation
A l'instant t = 0, deux barques B et B' naviguant sur un étang sont séparées d'une distance a. B se déplace sur l'axe Oy à la vitesse constante \(\overrightarrow{v}\) et B' se déplace parallèlement à l'axe (Ox) à la vitesse constante \(\overrightarrow{v'}\) comme le montre la situation ci-dessous.
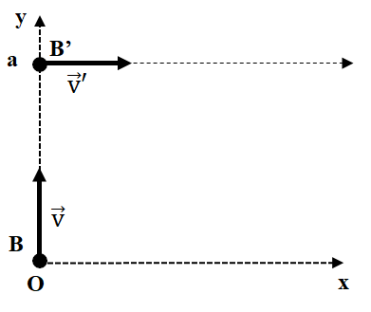
On appelle D la distance BB' entre les deux barques à l'instant t>0. D est une fonction de variable t. Au cours de leur parcours on suppose qu'il existe une distance minimale séparant les deux barques.
Lors du déplacement, quelle est la distance D minimale entre B et B'?
Explication Générale
Raisonnement :
D est minimal lorsque sa dérivée D'(t) s'annule pour t = \(t_{min}\), la distance minimale est alors : \(D (t_{min})\)
Il faudra :
Exprimer \(D(t)\)
Trouver \(t_{min}\) qui minimise \(D\)
Calculer la valeur \(D(t_{min})\)
Calculs :
Distance D(t) : Les coordonnées des deux barques à chaque instant sont : \(B(0 ; vt)\) et \(B'(v't ; a)\)
La distance est donc égale \(D=\sqrt{\left(x_{B'}-x_B\right)^2+\left(y_{B'}-y_B\right)^2}\)
On remplace par les coordonnées des points : \(D(t) = \sqrt{v'^2t^2+(a-vt)^2}\)
Dérivée : D est une fonction du type \(\sqrt{u}\) ; On dérive \(D(t) \)en utilisant la formule \((\sqrt{u})' = \frac{u'}{2\sqrt{u}}\)
On a donc : \(D ' (t) = \frac {2v'^2 t-2v(a-vt)}{2\sqrt {(v't)^2+(a-vt)^2}}\)
En simplifiant : \(D ' (t) = \frac {v'^2 t-2va+v^2t)}{\sqrt {(v't)^2+(a-vt)^2}}\)
Recherche du minimum : Il faut chercher le minimum de la fonction D, soit déterminer l'instant t pour lequel la dérivée de D par rapport à t s'annule : D'(t) = 0 pour \(v'^2 t_{min}-2va+v^2t_{min} = 0\)
soit \(t_{min}=\frac{av}{v^2+v'^2}\)
Le minimum de la fonction D est donc atteint pour \(t=\frac{av}{v^2+v'^2}\)
Valeur au minimum : Ce minimum est \(D\left(\frac{av}{v^2+v'^2}\right)=\sqrt{\left(\frac{avv'}{v^2+v'^2}\right)^2+\left(a-\frac{av^2}{v^2+v'^2}\right)^2}=\frac{av'}{\sqrt {v^2+v'^2}}\)
?Exprimer une grandeur à partir d'une relation
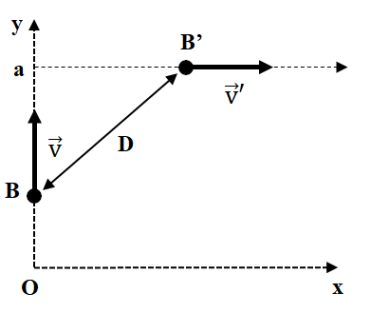
A l'instant t = 0, deux barques B et B' naviguant sur un étang sont séparées d'une distance a. B se déplace sur l'axe Oy à la vitesse constante \(\overrightarrow{v}\) et B' se déplace parallèlement à l'axe (Ox) à la vitesse constante \(\overrightarrow{v'}\) comme le montre la situation ci-dessous.

On appelle D la distance BB' entre les deux barques à l'instant t>0. D est une fonction de variable t. Au cours de leur parcours on suppose qu'il existe une distance minimale séparant les deux barques.

À quel instant t la distante D entre B et B' est-elle minimale ?
Explication Générale
Raisonnement :
D est minimal lorsque sa dérivée \(D'(t)\) s'annule pour\( t = t_{min}\).
Il faudra :
Exprimer \(D(t)\)
Trouver \(t_{min}\) qui minimise \(D\)
Calculs :
Distance D(t) : Les coordonnées des deux barques à chaque instant sont : \(B(0 ; vt)\) et \(B'(v't ; a)\)
La distance est donc égale \(D=\sqrt{\left(x_{B'}-x_B\right)^2+\left(y_{B'}-y_B\right)^2}\)
On remplace par les coordonnées des points : \(D(t) = \sqrt{v'^2t^2+(a-vt)^2}\)
Dérivée : D est une fonction du type \(\sqrt{u}\) ; On dérive \(D(t) \)en utilisant la formule \((\sqrt{u})' = \frac{u'}{2\sqrt{u}}\)
On a donc : \(D ' (t) = \frac {2v'^2 t-2v(a-vt)}{2\sqrt {(v't)^2+(a-vt)^2}}\)
En simplifiant : \(D ' (t) = \frac {v'^2 t-va+v^2t)}{\sqrt {(v't)^2+(a-vt)^2}}\)
Recherche du minimum : Il faut chercher le minimum de la fonction D, soit déterminer l'instant t pour lequel la dérivée de D par rapport à t s'annule : D'(t) = 0 pour \(v'^2 t_{min}-va+v^2t_{min} = 0\)
soit \(t_{min}=\frac{av}{v^2+v'^2}\)
Le minimum de la fonction D est donc atteint pour \(t=\frac{av}{v^2+v'^2}\)