Modèle exponentiel - Niveau 1
?Estimer les paramètres d'un modèle
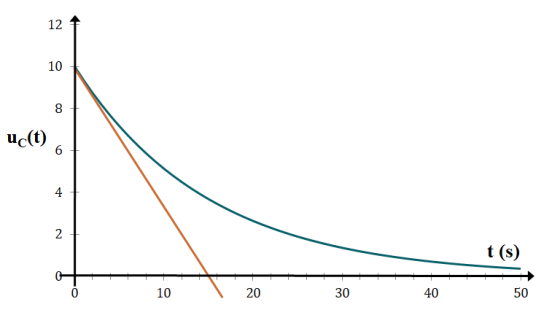
L'évolution temporelle de la tension \(u_{C}\) (unité : volt V) aux bornes d'un condensateur de capacité C lors de sa décharge dans un circuit RC est donné sur le graphe ci-dessous.
L'équation horaire de \(u_{C}\) est du type : \(u_{C}(t) = U_{0} \times e^{-\frac{t}{\tau}}\)
\(\tau\) est la constante de temps (unité: seconde s).
Quelle est la valeur de \(\tau\)?
Explication Générale
Raisonnement : Lors d'une évolution exponentielle, la valeur du temps caractéristique se lit au croisement de la tangente à l'origine et de l'asymptote de la courbe
Lecture graphique :
Dans ce cas, l'asymptote aux temps longs est l'axe des abscisses
La tangente à l'origine coupe l'axe des abscisses à t=15 s
Le temps caractéristique \(\tau\) de cette évolution est donc : \(\tau=15 \) s.
?Estimer les paramètres d'un modèle
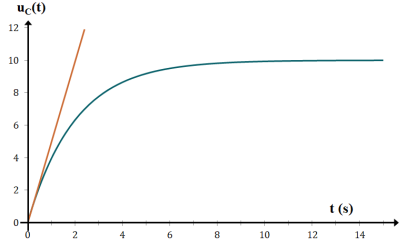
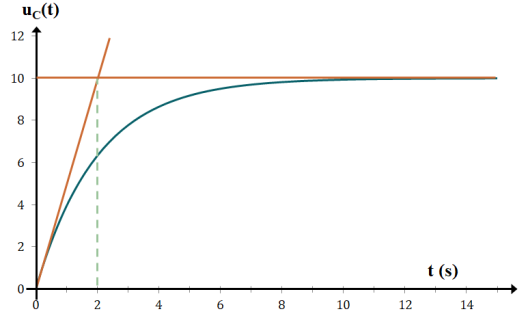
L'évolution temporelle de la tension \(u_{C}\) (unité : volt V) aux bornes d'un condensateur de capacité C lors de sa charge dans un circuit RC est donné sur le graphe ci-dessous.
L'équation horaire de \(u_{C}\) est du type : \(u_{C}(t) = U_{0} \times \left( 1 - e^{-\frac{t}{\tau}} \right)\)
\(\tau\) est la constante de temps (unité: seconde s).
Quelle est la valeur de \(U_{0} \)?
Explication Générale
Raisonnement : Lors d'une évolution exponentielle du type\( u_{C}(t) = U_{0} \times \left( 1 - e^{-\frac{t}{\tau}} \right)\) , la valeur de \(U_{0}\) correspond à l'asymptote aux temps longs.
Lecture graphique : l'asymptote aux temps longs est la droite \(u_{C}(t)\)= \(U_{0}\) = 10 V
?Estimer les paramètres d'un modèle
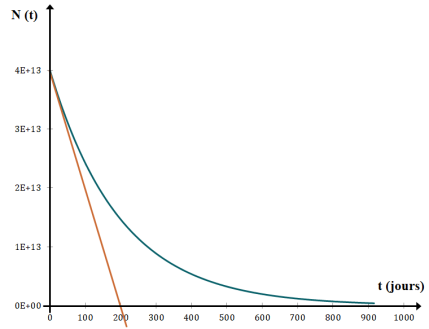
L'évolution temporelle du nombre de noyaux radioactifs du Polonium 210 \(N (t)\) est donné sur le graphe ci-dessous.
L'équation horaire de \(N (t)\) est du type : \(N (t) = N_{0} \times e^{-\frac{t}{\tau}}\)
\(\tau\) est la constante de temps (unité: jours).
Quelle est la valeur de \(\tau\)?
Explication Générale
Raisonnement : Lors d'une évolution exponentielle, la valeur du temps caractéristique se lit au croisement de la tangente à l'origine et de l'asymptote de la courbe
Lecture graphique :
Dans ce cas, l'asymptote aux temps longs est l'axe des abscisses
La tangente à l'origine coupe l'axe des abscisses à t=200 jours
Le temps caractéristique \(\tau\) de cette évolution est donc : \(\tau=200 \)jours.
?Estimer les paramètres d'un modèle
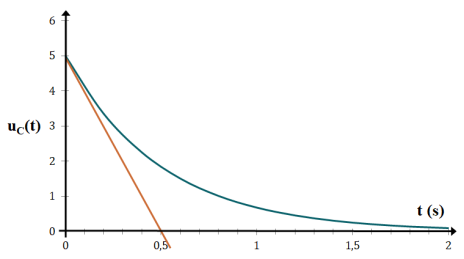
L'évolution temporelle de la tension \(u_{C}\) (unité : volt V) aux bornes d'un condensateur de capacité C lors de sa décharge dans un circuit RC est donné sur le graphe ci-dessous.
L'équation horaire de \(u_{C}\) est du type : \(u_{C}(t) = U_{0} \times e^{-\frac{t}{\tau}}\)
\(\tau\) est la constante de temps (unité: seconde s).
Quelle est la valeur de \(\tau\)?
Explication Générale
Raisonnement : Lors d'une évolution exponentielle, la valeur du temps caractéristique se lit au croisement de la tangente à l'origine et de l'asymptote de la courbe
Lecture graphique :
Dans ce cas, l'asymptote aux temps longs est l'axe des abscisses
La tangente à l'origine coupe l'axe des abscisses à t=0,5 s
Le temps caractéristique \(\tau\) de cette évolution est donc : \(\tau=0,5 \) s.